1.2.1 Mechanism FunctionThe Modeler2D package must be loaded before calling any Mech functions. This loads Modeler2D. Here is a graphic of the 2D slider-crank model.
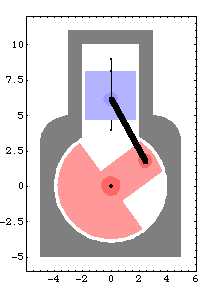
The following example analyzes the motion of a classic slider-crank mechanism. This mechanism is modeled with a simple and intuitive set of mechanical constraints that are representative of how such a problem would usually be modeled. Body NumbersThe slider-crank mechanism consists of three bodies.
Body 1 is the ground body.
Body 2 is the crankshaft.
Body 3 is the piston.Each independent body in a Mech model must be given a unique positive integer body number. The choice of each body number is arbitrary, except for the ground body, which must be body 1. These body numbers are used throughout a Mech model to reference each body. The ground body, which is stationary by definition, is used as the reference location and orientation for the rest of the model. All mechanism models must have some reference to the ground body to be adequately constrained.
To aid in the readability of the mechanism models created with Mech, a good practice is to name each of the bodies in a mechanism, and then define each of these names to be equal to the integer body number of the body. Each body can then be referenced by name instead of by a number. Body names are defined to be used as references for each body. A real slider-crank mechanism would have a fourth body, the connecting rod between the crankshaft and the piston. However, in the kinematic model this entire part can be replaced by a simple distance constraint specifying that the crank pin and the piston pin are a constant distance apart. This technique decreases the overall size of the model. Local CoordinatesEach body in a mechanism model must have a local coordinate system attached to it. How to place this coordinate system on the body is up to the user and is based on the needs of the model. It is not necessary to place the local coordinate origin at the center of gravity of the body. The local coordinate system of each body is used to define points, lines, and other features on the body that are then tied together to make the mechanical constraints.
The local coordinate system of body 1, the ground body, is always coincident with the global coordinate system. Therefore, the global coordinate system is referenced through the ground body, simply by specifying body 1.
|