1.3.4 Running the Model

A single command is used to solve the constraint equations and return the coordinates of each of the bodies the model.

The fundamental model-solving function.

This seeks a solution at crankangle = 0.

In[7]:=

Out[8]=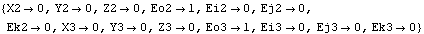

SolveMech returns the global coordinates of the origin of each body in the system. X2, Y2, and Z2 specify the location of the origin of body 2, the crankshaft.
Eo2, Ei2, Ej2, and Ek2 are the Euler generalized parameters specifying the angular orientation of the crankshaft. SolveMech returns a {Xn, Yn, Zn, Eon, Ein, Ejn, Ekn} set for each body in the system. For those unfamiliar with Euler parameters, suffice it to say that the four Euler parameters provide a numerically robust means of specifying the three degrees of freedom of the angular orientation of a body in 3D space. Values of {1, 0, 0, 0} for the four parameters, respectively, correspond to alignment with the global coordinate system. It is not necessary to have an understanding of the Euler parameters to utilize Modeler3D because postprocessing functions use the Euler parameters to generate more familiar output, such as the rotation of a body about an axis or the angle between two vectors. Euler parameters are discussed further in Chapter 4.

Here is a graphic of the slider-crank model at the initial configuration.

Not a very interesting solution! The solution at crankangle = 0 is for the local coordinate system of each body to be aligned with the global coordinate system. This is because the model was defined such as to have this perfect assembled configuration. The piston is defined such that its local origin lies at a point that is outside of the piston body. This point is coincident with the global origin when crankangle = 0. Note the 3-4-5 triangle formed by the crankshaft, piston, and connecting rod when crankangle = 0.
Advancing crankangle results in a more interesting solution.

This seeks a solution at crankangle = 1/10 revolution.

In[9]:=

Out[10]=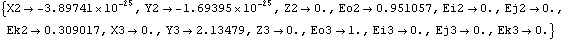

Now two of the Euler parameters of the crankshaft Eo2 and Ek2 have changed, and the vertical coordinate of the piston Y3 has increased to 2.13. All of the other coordinates have not changed, and never will, because of the specific function of this particular mechanism model.

This seeks a solution at crankangle = 3/10 revolution.

In[11]:=

Out[12]=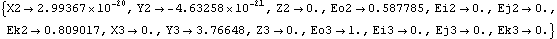

Here is a graphic of the model at crankangle = 3/10 revolution.