8.2.2 3D Example Mechanism

A Modeler3D example model is developed to demonstrate a simple gyroscopic inertial loading condition. The model is a flywheel with an angular velocity vector with a changing direction.
The model consists of only one moving body, the flywheel. The flywheel spins about an axis that is attached to the ground at one point. The axis of rotation of the flywheel is then rotated about another nonparallel axis affixed to the ground. Thus, the direction of the axis of rotation of the flywheel changes with time.

This loads the Modeler3D package.

In[1]:=

Here is a graphic of the flywheel model.

The Method -> Angular option is given to SetSymbols before building any other part of the flywheel model. This is done so that the angular velocity and angular acceleration of the flywheel is calculated directly, instead of being calculated in terms of derivatives of Euler parameters. Note that this is not a necessary step to obtain the dynamic forces.

This causes angular velocities to be calculated directly so that it won't be necessary to convert the Euler parameters into angular velocity.

In[2]:=

Inertia

The flywheel is modeled by four one-unit point masses, symmetrically placed about the axis of rotation. The Modeler3D CompositeInertia function can be used, trivially, to find the net inertia properties of the flywheel.

In[3]:=

Out[4]=

Bodies

One body object is defined for the flywheel model. The ground body does not have a body object because it has no inertia or required point definitions. The body object for the flywheel contains the inertia properties and the locations of each of the four point masses.

Names are defined for each of the body numbers in the model.

In[6]:=

Here is the body object for the flywheel.

In[8]:=

Constraints

Three constraints, two of which are functionally dependent on time, are required to model the flywheel mechanism.
A Spherical3 constraint places the center of the flywheel at the global origin.
A Parallel2 constraint forces the axis of rotation of the flywheel to be parallel with a specified vector on the ground body. The direction of the axis vector on the ground body is explicitly a function of time T. This constraint effectively causes the axis of rotation of the flywheel to change direction with time.
A ProjectedAngle1 constraint rotates the flywheel about its axis. Note the choice of the vector that was used on the ground body. The vector in the Y direction on the ground body is always normal to the axis of rotation of the flywheel. If a vector in the X direction was chosen instead, the constraint would become singular at T = 0.25. Note also that the flywheel is spinning 10 times more rapidly about its symmetry axis than its axis is rotating with respect to the ground.

Here are the constraint objects for the flywheel.

In[9]:=

Runtime

Because of the presence of T in the constraints, the model can be run through its intended range of motion by varying T directly with the SolveMech command.

Now run the model at T = 0.02.

In[10]:=

Out[10]=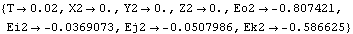

Here is the flywheel at T = 0.02.