8.2.3 Inertial Loading

No forces are applied to the model with SetLoads because only the inertial loading of the flywheel is being considered. All of the inertia properties have already been defined, so all that must be done to find the dynamic solution is to request it of SolveMech with the solution option.

The dynamic solution at T = 0.

In[11]:=

Out[11]=

The angular velocity and acceleration of the flywheel can be read directly from the solution rules returned by SolveMech, or Modeler3D output functions can be used. Note that the angular acceleration is orthogonal to the angular velocity.

Here are the angular velocity and acceleration of the flywheel.

In[12]:=

Out[12]=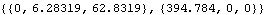

The moment that is applied to the flywheel to enforce the specified rotation is the reaction force to constraint 2, the constraint that controls the direction of the axis of the flywheel.
Note that the reaction to constraint 3 is zero. No moment is required to spin the flywheel about its primary axis, only to change the direction of the axis.

Here are the moments that are applied to the flywheel by the constraints.

In[13]:=

Out[13]=

In[14]:=

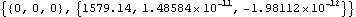Out[14]=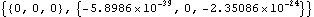

As the position of the flywheel is advanced in time, the components of the angular velocity change, and the components of the angular acceleration and the applied moment follow.

This calculates the dynamic solution at T = 0.01.

In[15]:=

Here are the angular velocity and acceleration.

In[16]:=

Out[16]=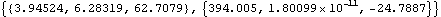

Here is the applied moment.

In[17]:=

Out[17]=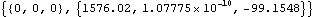