7.2.3 Running the Loaded Model

Because of the presence of T in the driving constraint cs[1], the model can be run through its intended range of motion by varying T directly with the SolveMech command. The numerical value of T specifies the distance between the bottom of the ladder and the wall.
Although loads have been added to the model, the SolveMech default option setting Solution -> Location solves only for the location variables.

Now run the model at T = 7.5.

In[17]:=

Out[17]=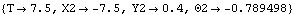

Mech must be told to solve for the static forces in the model with the Solution option for SolveMech.

An option for SolveMech.

The Solution -> Static option causes SolveMech to resolve the forces applied to the model into Lagrange multipliers.

Now run the model at T = 8.5.

In[18]:=

Out[18]=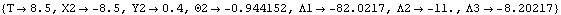

Here is the ladder-on-wall image at T = 8.5.

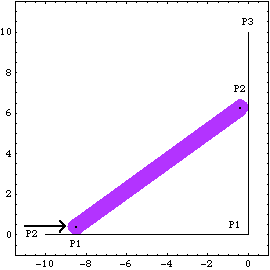
The numeric values of the Lagrange multipliers returned by SolveMech are not directly very useful, unless one has a very good understanding of the exact form of the constraints. However, the set of Lagrange multipliers associated with a mechanism model completely determines all of the reaction forces in the constraints in the model. To find the actual reaction forces and moments at a specific constraint it is necessary to use the Mech Reaction function, which is described in Section 7.3.