7.3 Resultant Forces

This section describes the usage of the two Mech functions that are used to convert the Lagrange multipliers into reaction forces on specific bodies in a model, Reaction and Loads.

7.3.1 2D Example Mechanism

To demonstrate the use of Mech's Reaction function, the 2D ladder-on-wall model that was developed in Section 7.2 is used. The bodies and constraints of the model are redefined here in abbreviated form.

The following loads the Modeler2D package and completely defines the ladder-on-wall model.

In[1]:=

In[4]:=

In[5]:=

The model is run to prove that it works.

In[6]:=

Out[6]=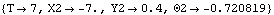

7.3.2 Reaction

The Reaction function is used to convert the Lagrange multipliers that are returned by SolveMech into specific reaction forces and moments that are applied to each body by the constraints in the mechanism model.

The function for finding constraint reaction forces.

An option for Reaction.

To demonstrate the use of Reaction, loads are applied to the ladder-on-wall model that was redefined in Section 7.3.1.

Here are the load objects for the ladder-on-wall model.

In[7]:=

Only the first two loads are added to the model initially; the other load will be added later. The model can then be run with the Solution -> Static option to solve for the Lagrange multipliers.

Load 1 and load 2 are applied to the current model.

In[10]:=

Now run the model at T = 6.0.

In[11]:=

Out[11]=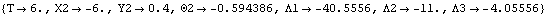

Because the Reaction function references constraints by number, names are given to each of the constraints for clarity.

Names are defined for each of the constraints in the model.

In[12]:=

The horizontal force at the bottom of the ladder that is required to hold the ladder in its current position is the reaction to constraint 1, the driving constraint. Note that the Y force and the moment sustained by the driving constraint are both zero, and always will be, because the driving constraint (RelativeX1) does not constrain motion in the Y or directions, therefore, it cannot sustain any load in those directions.

Here is the reaction to the driver.

In[17]:=

Out[17]=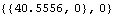

For the ladder to be in equilibrium, the force at the driver must be balanced by the force against the wall. Note that the Reaction function, like all other Mech output functions, returns a symbolic expression in terms of dependent variables.

Here is the reaction against the wall.

In[18]:=

Out[18]=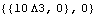

Out[19]=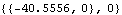

Note that if a different point is chosen about which to calculate the reaction, only the moment is changed. A reaction force is not a function of the point about which the reaction is calculated, therefore, the choice of a calculation point never affects the force, only the moment.

Here is the reaction against the wall calculated about a point on the ground.

In[20]:=

Out[20]=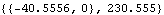

Since there is no friction in this model, the sum of all of the vertical forces is applied to the floor.

Here is the reaction against the floor.

In[21]:=

Out[21]=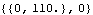

When the applied moment, load 3, is added to the model, it shows up as added reaction force against the driver and the wall.

The moment that was previously defined is added to the model.

In[22]:=

Here is the reaction against the wall.

In[23]:=

Out[23]=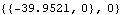

7.3.3 Loads

The actual load vector that is generated by SetLoads can be directly accessed with Loads. Loads can be very useful for debugging a model because it is often possible to read the load expressions directly and relate them to the function of the model.

The load inspection function.

An option for Loads.

If the Coordinates option is not specified, Loads returns forces that are generalized to the current velocity coordinate system. Since velocity in the current model is represented by {Xnd, Ynd, nd} the returned loads are {Fx, Fy, M}, calculated about the local origin. Consider the 2D ladder-on-wall model of Section 7.3.2. Loads can be used to find the total load applied to the ladder resolved into a force applied to the origin of the ladder, and a moment.

Here is the total load applied to the ladder.

In[24]:=

Out[24]=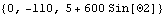

Out[25]=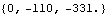

In all cases, the sum of the applied, reaction, and dynamic loads on any body must be zero. Since there are no dynamic loads in this model, the total reaction loads on all constraints must be equal to the total applied loads.

Here is the total reaction load applied by the constraints to the ladder.

In[26]:=

Out[26]=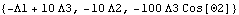

Out[27]=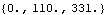

The dynamic, or inertial, loads on the ladder are identically zero because there are no masses or moments of inertia defined. If there were, the dynamic loads would be functions of the model's acceleration variables, X3dd, Y3dd, and so on.

Here are the inertial loads on the ladder.

In[28]:=

Out[28]=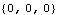

Note that the numerical sum of the loads is zero, but the algebraic terms are quite different. This basically shows part of the system of equations that was solved by SolveMech when the numeric values of the Lagrange multipliers were found.