3.4 2D Mechanism ImagesThis section demonstrates special Modeler2D graphics functions that are used to generate the mechanism images throughout this document. Modeler2D graphics functions return graphics primitives that are given as arguments to the Mathematica Graphics function and displayed with the Show command, just like the built-in Mathematica graphics primitives.
The primary utility of the Modeler2D graphics functions is that they take their arguments in the form of local coordinates and automatically convert them to global. Thus, it is possible to create the image of a mechanism part using the same techniques as would be used with built-in Mathematica graphics primitives, and then have the part be positioned properly with respect to the other parts of the mechanism automatically, as specified by a Modeler2D solution rule returned by SolveMech. 3.4.1 Graphics FunctionsThe Modeler2D graphics functions closely parallel the built-in Mathematica graphics primitives. Each graphics function generates Mathematica graphics primitives that represent points, lines, or polygons. Basic Mech graphics function. More 2D graphics functions. Options for graphics functions. The Modeler2D Vertex, Edge, and Facet functions are analogous to the built-in Mathematica Point, Line, and Polygon functions. To demonstrate these functions, graphics objects are generated that are located on body 2, which is named body2. This loads the Modeler2D package. Here is a box with a diagonal and a couple of points. The coordinates of the graphic just created bdgraph are functions of the Modeler2D variables that locate body2: X2, Y2, and  2. Therefore, these variables must be replaced with numeric values before the graphic can be displayed with Show. This shows bdgraph rotated 0.5 radians counterclockwise.
Out[5]= |  |
This shows bdgraph rotated 1 radian and translated 1 unit to the right.
Out[6]= |  |
The Box function is analogous to the built-in Rectangle function, with the exception that the sides of the Box graphic are aligned with the local coordinate system in which the graphic is located, instead of being aligned with the global coordinate system.
The Bar function also generates a rectangular box, but instead of specifying two points on two opposite corners, two points on two opposing sides of the rectangle are specified. The Faces option is used with the Bar function to show only an outline of the bar. Unlike the Box function, Bar accepts an axis object as its first argument, to allow the two endpoints of the bar to lie on two different bodies. Here is a Box graphic on body2 and a Bar graphic spanning from body2 to the ground, with an Edge graphic down the middle. Here is the result.
Out[8]= |  |
The Wheel function is used here to generate an octagon with a hole in it. Note that the n-gon returned by Wheel is placed on the body that is referenced in the Point argument, and is located with that body as such. This generates an octagon on body2. Here is the result.
Out[10]= |  |
3.4.2 Annotation FunctionsThree graphics functions are provided by Modeler2D specifically for annotation. Graphics functions for annotation. PointLabel and LocalAxes can be used to conveniently label points and bodies. The following input generates a triangle placed on body 2, with two of the points labeled with their body numbers and local coordinates. This generates a labeled triangle on body2. Here is the result.
Out[13]= |  |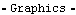
A function for plotting the locus of a moving point. The nested list of rules required by LocusPlot is of the form returned by SolveMech when given a range of times at which to seek solutions. 3.4.3 Example Mechanism GraphicsThe quick-return mechanism model that was developed in Section 3.1 is used to demonstrate the Modeler2D graphics functions. The model is redefined as follows in abbreviated form. The complete quick-return model. To demonstrate the use of the graphics functions, the image of the quick-return mechanism that was displayed in the preceding sections is built. These images are generated with a mix of Modeler2D graphics functions and built-in Mathematica graphics primitives. GroundThe ground body of the quick-return mechanism is generated using Modeler2D graphics functions even though it does not move. This is done to take advantage of the easy referencing of local point coordinates that were defined with SetBodies. Note that the Edge function in the following graphic references points either by their {x, y} coordinates or by their local point numbers interchangeably. Here is the ground body graphic. The text that is shown with the ground body is generated entirely with the built-in Mathematica Text function. Here is the ground body graphic annotation. Here is the result.
Out[22]= |  |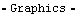
CrankThe crank graphic uses only built-in Mathematica graphics functions, with the exception of the Vertex function to plot two local points on the crank, the coordinates of which are defined in a body object. Note the use of the Location function inside of the Disk primitives. This places the disks at the correct global coordinates when the crank moves. Here is the crank body graphic. The text that is displayed with the crank graphic also uses the Location function to specify the global coordinates of the text so that the text moves with the crank. Here is the crank graphic annotation. Because the coordinates of some of the elements in crankgraphic and cranktext are now functions of Modeler2D dependent variables X2, Y2, and 2, a Modeler2D solution rule must be applied before they can be displayed. Note the use of SolveMech in the following input. Here is the result.
Out[25]= |  |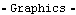
Drive ArmThe drive arm graphic uses mostly built-in Mathematica graphics functions. Note how the Bar and Vertex function are called using local points 1 and 2, while the Edge function is called with explicit local point coordinates {0, 2} and {0, 8}. Most Mech functions attempt to interpret integers as local point numbers and resolve them into coordinates. Here is the drive arm graphic. The text that was displayed with the drive arm graphic also used the Location function to specify the global coordinates of the text so that the text moves with the drive arm. Here is the drive arm graphic annotation. Like the crank graphic, the coordinates in the drive arm graphic are functions of Modeler2D dependent variables. Thus, a solution rule must be applied to display the graphic. Here is the result.
Out[28]= |  |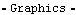
SliderThe slider graphic uses just one built-in Mathematica graphics primitive and one Modeler2D graphics function. Here is the slider graphic. Here is the slider annotation. Here is the result.
Out[31]= |  |
Connecting RodThe connecting rod graphic is nothing more than a line connecting two points on two different bodies. Here is the connecting rod graphic. To show the complete quick-return mechanism, all of the graphics objects are combined and displayed subject to a single Modeler2D solution rule. Here is the complete mechanism at T = 0.15.
Out[33]= |  |
Here is the mechanism at T = 0.55.
Out[34]= |  |
| 
