9.2 Multiple Configuration CouplesThe SetCouple and SolveCouple functions can be used to find the values of several parameters that simultaneously satisfy several geometric conditions at different configurations of the model, at different points in time. 9.2.1 Solving for Two ParametersBuilding coupled systems across multiple configurations. The InitialGuess and Time options are used somewhat differently than standard Mathematica option usage because one specification for time and one set of initial guesses must be given for each separate mechanism configuration. The Time option must be specified for a multiple configuration CoupleSystem because the default setting sets the value of time to be the same for all configurations, making all configurations identical. Since the Compiled option applies to the entire CoupleSystem, it can appear in any part of the SetCouple command.
The following example uses the four-bar model that was developed in Section 9.1. A coupled system is used to adjust the lengths of both the drive and driven bars so as to meet two geometric conditions that are satisfied at two different points in time. The X coordinate of point 3 on the center bar is set to 0.8 at T = 0.1, and the distance from the global origin to point 2 on the center bar is set to 3.8 at T = 0.3.
Because the coupled system is simultaneously solved in two different mechanism configurations, the same initial guess for both configurations may not be acceptable. Therefore, the InitialGuess option is used to explicitly specify initial guesses for each configuration. Here are two initial guesses for the two configurations. Here are parts of the two conditions at the two initial configurations.
Out[41]= | 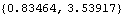 |
This builds the CoupleSystem object. A CoupleSystem object that spans multiple configurations has a unique solution at each configuration. Thus, SolveCouple returns a nested list of solution rules with each list corresponding to one configuration of the mechanism. This solves the CoupleSystem object and finds new values for bar2 and bar3.
Out[43]= |  |
This shows that the desired condition is satisfied.
Out[44]= | 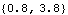 |
9.2.2 Solving for Multiple ParametersIt is possible to specify any number of geometric conditions to be satisfied at any number of different mechanism configurations, however, it is certainly not possible to satisfy any arbitrary set of conditions. A CoupleSystem object built by SetCouple may have no solution, or it may have stiff singularities at points very close to a valid solution, making it difficult to converge the model. The following example demonstrates a useful technique for slowly coaxing a model towards a desired solution with SolveCouple.
In the following example, a coupled system is used to find the values of bar2, bar3, bar4, and T that satisfy four different geometric conditions at two different points in time. The X and Y coordinates of point 3 on the center bar are specified at T = 0.1, and the X and Y coordinates of point 3 on the center bar are specified at an arbitrary time T > 0.1, effectively specifying that point 3 on the center bar must pass through a given point in the global reference frame. Here is the current location of point 3 at T = 0.1 and T = 0.3.
Out[46]= | 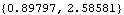 |
Out[47]= | 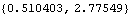 |
First, a CoupleSystem object is built that has very unambitious goals. This system simply tries to satisfy a set of conditions that are already approximately satisfied. Then, the coordinate goals k1, k2, k3, and k4 are changed, slowly pulling the solution of the model away from its original configuration. The new parameters, k1 to k4, are added to the parameters list. Note that the parameters bar2, bar3, and bar4 are approximately equal to their original values.
Out[50]= | 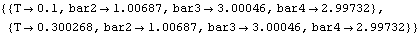 |
When SolveCouple is called with a symbol that evaluates to a CoupleSystem object as its first argument, SolveCouple updates the initial guesses contained within the CoupleSystem object to the new values found to be the solution. Therefore, independent parameters can be slightly tweaked between successive runs of SolveCouple, with each run nudging the model slightly closer to the desired solution. The parameters are repeatedly changed and the model is re-solved.
Out[52]= | 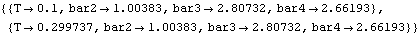 |
Out[54]= | 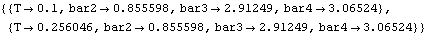 |
Out[56]= | 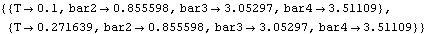 |
Out[58]= | 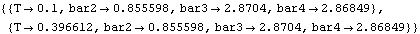 |
Here is the four-bar mechanism at T = 0.1 and T = 0.396, with the locus of point 3 on the center bar.
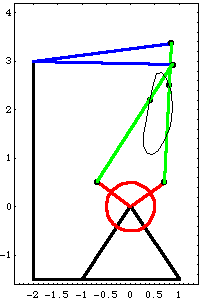
The k1-k4 parameters are removed from the parameters list.
|