12.4.1 2D Coordinate Systems

There is no clear rule for the best choice of coordinate systems in planar or spatial models, with respect to minimizing run time. In 2D, it would seem that Angular would always be better, because only three constraint expressions are required per body, instead of four. But, this is largely offset by the fact that the 2D degenerate Euler coordinate system uses no trigonometric functions in the formulation of geometric constraints, and that the first and second derivatives of expressions written in terms of 2D Euler parameters are very simple.

This sets the 2D coordinate system to Angular and defines a bogus constraint so that the symbolic derivatives of the coordinates of body 2 are defined by SetConstraints.

In[1]:=

Here are the location and velocity of an arbitrary point in angular coordinates.

In[5]:=

Out[5]=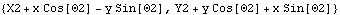

Out[6]=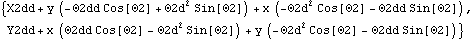

Now the coordinate system is changed to Euler.

In[7]:=

Here are the location and velocity of an arbitrary point in 2D Euler coordinates.

In[9]:=

Out[9]=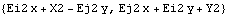

Out[10]=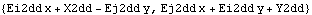

In conclusion, models that are to be used for acceleration analysis may run faster if the degenerate Euler coordinates are used, but they may not.