12.4 Coordinate SystemsMechanicalSystems allows models to be built in several different coordinate systems: Euler and Angular in two dimensions, and Euler, Global Angular, and Local Angular in three dimensions. If the mechanism is planar, use a planar model because 2D models run much faster than 3D models. 12.4.1 2D Coordinate SystemsThere is no clear rule for the best choice of coordinate systems in planar or spatial models, with respect to minimizing run time. In 2D, it would seem that Angular would always be better, because only three constraint expressions are required per body, instead of four. But, this is largely offset by the fact that the 2D degenerate Euler coordinate system uses no trigonometric functions in the formulation of geometric constraints, and that the first and second derivatives of expressions written in terms of 2D Euler parameters are very simple. This sets the 2D coordinate system to Angular and defines a bogus constraint so that the symbolic derivatives of the coordinates of body 2 are defined by SetConstraints. Here are the location and velocity of an arbitrary point in angular coordinates.
Out[5]= | 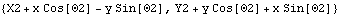 |
Out[6]= | 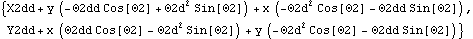 |
Now the coordinate system is changed to Euler. Here are the location and velocity of an arbitrary point in 2D Euler coordinates.
Out[9]= | 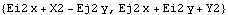 |
Out[10]= | 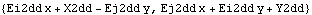 |
In conclusion, models that are to be used for acceleration analysis may run faster if the degenerate Euler coordinates are used, but they may not. 12.4.2 3D Coordinate SystemsIn 3D models, there is no difference between the respective coordinate systems with regard to the constraint equations alone because all 3D models must use Euler parameters to represent the angular orientation of each body. Thus, the choice of coordinate systems comes down to differences in first- and second-order expressions, and in the dynamic equations of motion.
As with 2D coordinates, the first and second derivatives of expressions written in terms of 3D Euler parameters are simpler than the same expressions written in terms of angular velocities and accelerations. This sets the 3D coordinate system to Angular and defines a bogus constraint so that the symbolic derivatives of the coordinates of body 2 are defined by SetConstraints. Here are the location and velocity of an arbitrary point in angular coordinates.
Out[14]= | 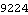 |
Now the coordinate system is changed to Euler. Here are the location and velocity of an arbitrary point in Euler coordinates.
Out[17]= | 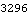 |
However, the relative sizes of the expressions generated by applied forces and moments in a static or dynamic model are also affected by the choice of coordinate system. Usually, the expressions that are generated by applied forces and moments are simpler in angular coordinates than they are in Euler coordinates. Here is the expression that results from an applied moment in angular coordinates.
Out[21]= | 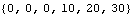 |
Here is the expression that results from the same applied moment in Euler coordinates.
Out[25]= | 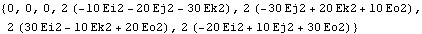 |
However, here is the expression that results from the same applied moment in local angular coordinates.
Out[29]= | 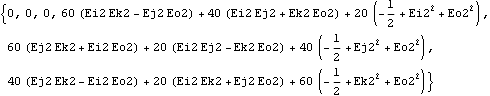 |
If this is not yet sufficiently murky, consider that if the applied moment in the previous example was specified as a constant moment in local coordinates on body 2, the conditions of the moment expressions in local versus global angular coordinates would be reversed. The moment would be a constant in local coordinates and a function of the Euler parameters in global coordinates.
In conclusion, the fastest run times usually result from matching the coordinate system to the types of applied forces and moments on the body. If the applied loads are in global coordinates, use the global coordinate system, and visa versa.
|