12.2.1 Local Coordinate Choices

MechanicalSystems allows considerable flexibility in defining geometric constraints and forcing functions. The points and lines that are used to make up these elements can be located anywhere in the local coordinate system of any body in the model. However, all points are not created equal, in terms of efficiency, and choosing a more complicated representation of a geometric relationship over a simpler one can result in large changes in the time required to run a model.
In general, it is best to use the local origin of a body whenever possible in defining constraint or load functions because the local origin is represented by a much simpler expression than a non-origin point. When the local origin cannot be used, the more zeros there are in the local coordinates of a point, the better.

Here are the symbolic representations of three points on the crank.

In[12]:=

Out[12]=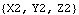

Out[13]=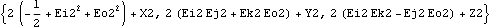

Out[14]=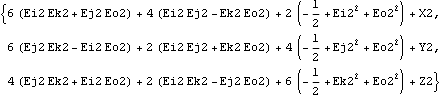

Obviously, it takes less time to evaluate the first of these three expressions than it does to evaluate the others. Further, since all points on the ground body are constant, use points on the ground body over points on other bodies whenever possible, even over the local origins of the other bodies.
These guidelines also apply to the definition of Line, Plane, and Axis objects; use the ground body if possible. However, it is usually better to use two or three points on the same body to define a Line or Plane object than it is to use one point on the ground and other points on another body.
Finally, one point where the relative simplicity of the local origin is of great importance is in the location of the centroid of a dynamic model. While Mech does allow the centroid to be placed arbitrarily on a body, moving the centroid off of the local origin of a body results in a great increase in the complexity of the model's mass matrix. The mass matrix of a 3D body in local coordinates is a block diagonal constant matrix (completely diagonal if the products of inertia are zero), if the centroid is located at the local origin. If the centroid is moved off of the local origin, the mass matrix becomes a 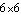nonconstant full matrix. This is especially important when integrating the equations of motion, when the mass matrix must be evaluated at every time step.