12.2 Simplifying ExpressionsThis section covers some of the ways that a MechanicalSystems model can be algebraically simplified to improve performance. 12.2.1 Local Coordinate ChoicesMechanicalSystems allows considerable flexibility in defining geometric constraints and forcing functions. The points and lines that are used to make up these elements can be located anywhere in the local coordinate system of any body in the model. However, all points are not created equal, in terms of efficiency, and choosing a more complicated representation of a geometric relationship over a simpler one can result in large changes in the time required to run a model.
In general, it is best to use the local origin of a body whenever possible in defining constraint or load functions because the local origin is represented by a much simpler expression than a non-origin point. When the local origin cannot be used, the more zeros there are in the local coordinates of a point, the better. Here are the symbolic representations of three points on the crank.
Out[12]= |  |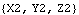
Out[13]= |  |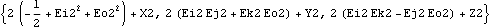
Out[14]= |  |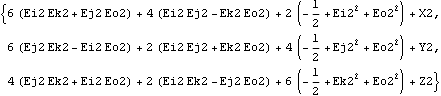
Obviously, it takes less time to evaluate the first of these three expressions than it does to evaluate the others. Further, since all points on the ground body are constant, use points on the ground body over points on other bodies whenever possible, even over the local origins of the other bodies.
These guidelines also apply to the definition of Line, Plane, and Axis objects; use the ground body if possible. However, it is usually better to use two or three points on the same body to define a Line or Plane object than it is to use one point on the ground and other points on another body.
Finally, one point where the relative simplicity of the local origin is of great importance is in the location of the centroid of a dynamic model. While Mech does allow the centroid to be placed arbitrarily on a body, moving the centroid off of the local origin of a body results in a great increase in the complexity of the model's mass matrix. The mass matrix of a 3D body in local coordinates is a 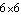 block diagonal constant matrix (completely diagonal if the products of inertia are zero), if the centroid is located at the local origin. 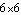If the centroid is moved off of the local origin, the mass matrix becomes a  nonconstant full matrix. This is especially important when integrating the equations of motion, when the mass matrix must be evaluated at every time step. 12.2.2 Constraint and Load ChoicesThe entire set of constraint functions provided by Mech is quite redundant. Almost any geometric constraint can be duplicated by some other constraint or combination of constraints. However, the algebraic expressions generated by functionally identical constraints can be quite different. It is important to use the simplest possible representation of a mechanism joint to reduce the size of the model.
The one time when a more complicated constraint set should be considered is when it is possible to remove a body from a model by replacing the entire body with a compound constraint. The OrthoRevolute4 and ParaRevolute4 constraints in Modeler3D are good candidates for replacing entire bodies in a model, as is the RelativeDistance1 constraint that is commonly used to replace a connecting rod. It is often possible to eliminate multiple bodies, even interlinked bodies, with a correctly chosen compound constraint.
A body cannot be eliminated from a mechanism when the inertia of the body is relevant to the analysis. But even this has an exception: the gyroscopic forces associated with a body that is spinning rapidly about an axis of symmetry can be duplicated by a GyroMoment forcing function, thus eliminating the body itself from the model. 12.2.3 Simplifying with MathematicaAfter the constraints and loads used to build the Mech model have been chosen as carefully as possible to simplify the model, Mathematica's Simplify or Expand functions can be applied to all of the internal expressions generated by Mech by setting $MechProcessFunction equal to Simplify, Expand, TrigExpand, or any other routine designed to simplify expressions or optimize them for efficient evaluation.
Because many of the internal expressions generated by MechanicalSystems are very large, applying Simplify to all of them can be quite computationally expensive in itself. The performance of SetConstraints and related model-building functions can be degraded significantly in exchange for better performance from SolveMech. This will cause Simplify and Chop to be applied to all internal expressions generated by Mech.
Out[15]= |  |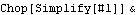
|
