10.4.1 Numerical IntegrationNumerical integration with SolveFree. There are several issues that are specifically associated with the numerical solution of the constrained equations of motion generated by MechanicalSystems. The equations of motion are a nonminimal differential-algebraic system of equations, that may or may not be linear in the highest-order terms.
One important issue is constraint violation. The equations of motion do not include the actual kinematic constraints, they only include the second time derivatives of the constraint equations. Because of this, small errors in the numerical integration of the equations of motion can accumulate into large violations of the kinematic constraints and their first derivatives. To deal with this problem, the equations can be algebraically reduced to a minimal set, but this is not generally possible with the type of constraints allowed by Mech. Alternatively, the numerical values of the dependent variables can be corrected as the integration progresses so as to continuously satisfy the constraints. This method is implemented in SolveFree.
Another issue is the transformation of angular velocity and acceleration in 3D models. If a model is built with angular coordinates (the Method -> Angular option in SetSymbols) the first and second derivatives of angular orientation are represented by the angular velocity, omega, and the angular acceleration, alpha. Unfortunately, omega is not the first derivative of the Euler parameters used to represent angular orientation. Thus, a coordinate transformation must occur at each time step to allow the Euler parameters to be integrated. SolveFree handles this transformation automatically, so models built in any coordinate system can be integrated.
The equations of motion are not necessarily linear in their highest-order terms, depending on the form of the applied loads. SolveFree automatically switches to an iterative solution method for nonlinear systems that allows them to be solved, albeit slowly. Initialization OptionsThe only option that is concerned with the initialization of the integrator is the InitialCondition option. All other information needed to integrate the equations of motion is contained in the FreeSystem object. This option is most useful for repeatedly integrating the same FreeSystem with different sets of initial conditions without having to rerun SetFree. An initialization option for SolveFree. The list of rules required by InitialCondition is of the form returned by SolveMech. Using SolveMech to generate the initial conditions (which is essentially what is done by the default setting) guarantees that the initial conditions constitute a valid solution to the constraint equations. If initial conditions that do not satisfy the constraints are passed to SolveFree, the integration will proceed without difficulty, producing results that satisfy the differential equations of motion, but do not satisfy the kinematic constraints.
Note that a sufficient set of initial conditions for integrating a free acceleration system is returned by SolveMech[time, Solution -> Velocity], while a sufficient set of initial conditions for integrating an equilibrium velocity system is returned by SolveMech[time]. Integration OptionsThe following options are used to control the actual integration algorithm used by SolveFree. The default settings for these options are intended to produce reasonable results in the shortest possible time with a well-behaved system. Some tweaking may be required to get the best result from models with large accelerations or force discontinuities. Options for controlling the SolveFree integrator. More options for controlling the integrator. The error estimation used by SolveFree makes an assumption that the approximate magnitude of each of the dependent variables is near to 1. While this assumption is certainly valid for Euler parameters that are between -1 and 1, and the 2D angular coordinate that has units of radians, it is up to the user to choose a system of units such that the linear dimensions of the model are not extremely large or small. While the error estimation routine does not look at the Lagrange multipliers (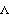 1, 1, 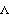 2, ...) it is best to keep the units of force and mass such that the Lagrange multipliers are not extremely large or small, because other parts of the numerical solution method begin to produce significant errors when dealing with a wide range of numerical magnitudes. 2, ...) it is best to keep the units of force and mass such that the Lagrange multipliers are not extremely large or small, because other parts of the numerical solution method begin to produce significant errors when dealing with a wide range of numerical magnitudes.
When step size switching is enabled, SolveFree basically limits the maximum error in any dependent variable at a single time step to be less than the MaxError setting. If this is exceeded at a time step, the integrator backs up, halves the step size, and proceeds forward again. This error limit seems rather loose. If the same variable exhibited the maximum signed error at each time step, the cumulative error in that variable after 1000 time steps would be 0.1! In reality, the large errors occur at discrete points in the motion of a model, so the cumulative error is normally smaller.
The MaxError option can also be used to explicitly specify the error magnitude limits at which the time step size is halved, doubled, or when a corrective versus predictive step is taken. MathError -> {a, b, c} specifies that the time step size will be doubled if the sum of the maximum errors in the last four steps drops below c, it will be halved if the error in the current step goes above a, and an Adams-Moulton corrective step will be taken if the error is between a and b. Thus, MaxError -> {0.0001, 0.00001, 0.000001} is equivalent to the default setting of MaxError -> 0.0001. Iterative Solution OptionsThe following options are used only to control the iterative solution block used for nonlinear models. These options have no effect on linear models. Options for the Newton-Rhapson solution block in SolveFree. Free acceleration models are always linear in the acceleration variables (X2dd, Y3dd, ...) but they may be nonlinear in the Lagrange multipliers (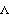 1, 1, 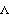 2, ... ) if there are loads applied that are algebraically dependent on reaction forces, such as friction. Equilibrium velocity models can be nonlinear in the Lagrange multipliers, and they can also be nonlinear in velocity variables (X2d, Y3d, ...) if the applied loads are nonlinear functions of velocity. The second element in a FreeSystem object tells whether the model is linear or not. FreeSystem[...][[2]] returns True for nonlinear models. 2, ... ) if there are loads applied that are algebraically dependent on reaction forces, such as friction. Equilibrium velocity models can be nonlinear in the Lagrange multipliers, and they can also be nonlinear in velocity variables (X2d, Y3d, ...) if the applied loads are nonlinear functions of velocity. The second element in a FreeSystem object tells whether the model is linear or not. FreeSystem[...][[2]] returns True for nonlinear models. Output Control OptionsThe following options are used to determine what data is returned by SolveFree, and what format is used to returned it. Output options for SolveFree. The StepSize data returned by the Diagnostics setting can be useful to help determine what should be chosen for a constant step size, if one is desired. The MaxError data included by Diagnostics is the measure of error used by the adaptive time step adjustment algorithm to decide when to change the step size.
|