4.2.2 Output FunctionsWhile Mech provides a wide array of output functions that return various quantities related to body location or orientation, only a small subset of those output functions are available in versions that are related to body velocities or accelerations. The most basic of those are the two higher-order analogies of the Location function. For each of the following functions, the point argument can be a Mech point object or just the arguments to a Mech point object. Velocity and acceleration output functions. The velocity of the steering tie rod attachment point on the wheel carrier is very near zero in the global reference frame because the chassis is allowed to move up and down while the bottom of the tire (the carrier body) remains in contact with the ground. Thus the motion of the carrier with respect to the ground is just a small tipping about the bottom of the tire. This calculates the velocity of a point.
Out[6]= | 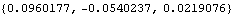 |
A related velocity function. The velocity of the steering tie rod attachment point with respect to the chassis has a much larger vertical component, while the longitudinal and transverse components remain the same. The velocity of a point, relative to another body, is shown here.
Out[7]= | 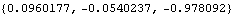 |
Two functions provide the higher-order analogies to the Rotation function. 2D2D angular velocity and acceleration functions. 3D3D angular velocity and acceleration functions. Note that all Mech output functions formulate expressions in terms of derivatives of Euler parameters, or global angular velocities and accelerations, or local angular velocities and accelerations. Which form is returned depends on the settings of the Method and Coordinates options for SetSymbols that were in effect the last time that the model was built.
For example, the current model was built with the default Method -> Euler setting in SetSymbols; therefore, all output functions will return expressions in terms of derivatives of Euler parameters that can be replaced by a solution rule. Here is the angular velocity of the wheel carrier.
Out[8]= | 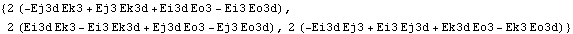 |
Out[9]= | 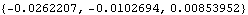 |
The Method -> Angular option is now used with SetSymbols. This changes the formulation of the Modeler3D output functions, but the numbers remain the same. The model is rebuilt with the Angular option setting. The angular velocity of the wheel carrier is the same.
Out[12]= | 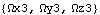 |
Out[13]= | 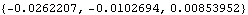 |
Again, the internal representation of the angular velocity can be changed to local coordinates, but the numerical results from the output functions remain the same. The model is rebuilt again with local angular velocity representation. The angular velocity of the wheel carrier is still the same.
Out[16]= | 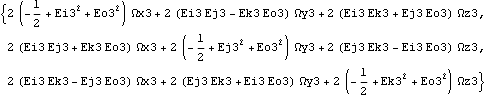 |
Out[17]= | 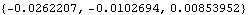 |
The only other output functions that are defined by Mech are the higher-order analogies to the Distance function. These two functions are defined largely for academic reasons, because they can be reproduced simply by differentiating the Distance function, as is shown in Section 4.2.3. Two more higher-order output functions. There is a slight difference between using the velocity output functions Velocity, DDistanceDT, and so on, and simply differentiating their first-order counterparts Location and Distance. The first- and second-order output functions use the Mathematica D operator to differentiate the local coordinates of each point, thereby assuming that the local coordinates are constant unless they are explicitly functions of time T. Here are the length, and the first and second derivatives of the length of the strut.
Out[18]= | 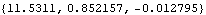 |
|