4.2.3 Differentiating ExpressionsAlthough Mech provides only a small number of predefined output functions that relate to velocity and acceleration, any expression that is written in terms of Mech dependent variables can be differentiated with Dt because definitions have been automatically made for Dt[X, T], where X is any Mech dependent variable. Now the model is rebuilt with the Method -> Euler setting. Here is the rate of change of the camber angle.
Out[21]= | 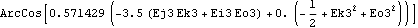 |
Out[22]= | 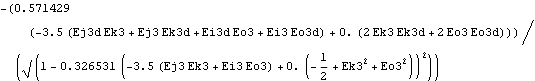 |
This generates a numerical result at T = 2.5.
Out[23]= | 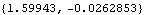 |
Note that Dt automatically replaced derivatives of dependent variables with the appropriate symbols. This form of differentiation is valid even when crossing from Euler to angular coordinates.
Consider the following example. With the Method -> Euler setting for SetSymbols, differentiating the seven Modeler3D location coordinates associated with body 3 with respect to T has the apparent effect of appending a d to the name of each variable. These new symbols are explicitly included in the solution rules returned by SolveMech.
However, with the Method -> Angular option set, differentiating the seven Modeler3D symbols with respect to T produces different symbolic results. This shows the functional relationship between the Euler parameters and the angular velocity. After replacement with a SolveMech solution rule, the results are numerically identical. This shows the derivatives of dependent variables.
Out[24]= | 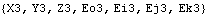 |
Out[25]= | 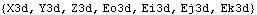 |
Out[26]= | 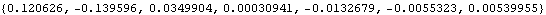 |
Now the model is rebuilt with the Method -> Angular option. The derivatives of dependent variables have changed form, but their values remain the same.
Out[29]= | 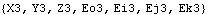 |
Out[30]= | 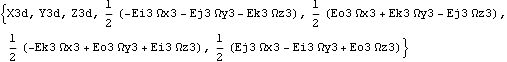 |
Out[31]= | 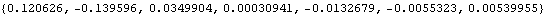 |
The same holds true for the local coordinate formulation.
Out[34]= | 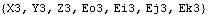 |
Out[35]= | 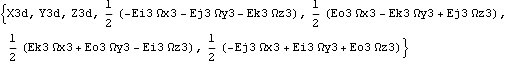 |
Out[36]= | 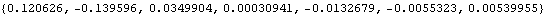 |
Note that the only difference between the derivatives of the Euler parameters in terms of global or local coordinates is that a few of the signs are swapped.
|