4.2.4 Euler's Angles

As shown in Sections 4.2.2 and 4.2.3, Euler parameters and their derivatives are directly related to the angular velocity vector of a spatial body, and a direct conversion between angular velocity and the derivatives of Euler parameters is possible. However, there is no vector representation of spatial angular orientation so other representations must be used.
One method of representing the angular orientation of a spatial body is to define a sequence of three finite rotations about three fixed axes that take a body from one orientation to another. These three rotations are called Euler's angles. Angular orientations represented by Euler's angles are readily converted to and from Euler parameters with a combination of Modeler3D output functions. Mech does not provide a single function to make this conversion, because there are many possible combinations of successive rotations that can be used to represent the angular orientation of a body.
The following example shows the general procedure required to convert an angular orientation from a sequence of finite rotations to a set of Euler parameters. In this particular case, the sequence of rotations are the most commonly used Euler's angles.

Here are the three rotation angles, and vector constants for each axis.

In[37]:=

A single rotation matrix that combines the three successive rotations is created by multiplying the rotation matrices associated with each.

In[43]:=

Out[43]//MatrixForm=

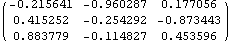The EulerParameters function is used to convert the rotation matrix to a set of Euler parameters.

In[44]:=

Out[44]=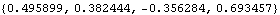

The conversion of Euler parameters to a sequence of finite rotations is not such a straightforward process. The general procedure is to measure the angle between an appropriate pair of axes located in the global and local reference frames. The following example shows how to convert the Euler parameters eulpars back to three Euler's angles.

Since Mech output functions that return expressions in terms of the symbolic Euler parameters are used, a list of replacement rules is needed.

In[45]:=

Out[45]=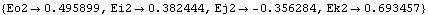

Here is the second Euler's angle theta. It is the included angle between the two Z axes in the global and local reference frames.

In[46]:=

Out[46]=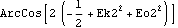

Out[47]=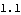

Here is the first Euler's angle phi. It is the angle between the local Z axis and the global -Y axis, as viewed looking down onto the global X-Y plane.

In[48]:=

Out[48]=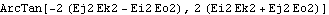

Out[49]=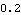

Here is the last Euler's angle psi. It is the angle between the local Y axis and the global Z axis, as viewed looking down onto the local X-Y plane.

In[50]:=

Out[50]=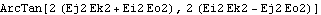

Out[51]=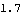

Any angular orientation can be represented by a single finite rotation about a fixed axis. This single rotation angle and axis are directly related to the Euler parameters so a direct conversion can be made with the Rotation function.

Here is the single rotation about a fixed axis that is equivalent to the three successive rotations phi, theta, and psi.

In[52]:=

Out[52]=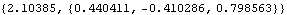

Some readers may be more familiar with the use of quaternions to represent the orientations of spatial bodies. Quaternions are four-dimensional complex quantities, with associated rules for multiplication, that allow them to be used much like 3D rotation matrices. The numerical values of the four elements of the quaternion qw + qx i + qy j + qz k are equivalent to the numerical values of the four Euler parameters {eo, ei, ej, ek} representing the same orientation. Quaternions and Euler parameters are notationally and conceptually quite different, but they are computationally equivalent.