If a multi-input, multi-output (MIMO) system described by a p × p transfer-function matrix G(s) is diagonal dominant over the bandwidth of interest, or can be made to be diagonal dominant by the use of an appropriate input compensator matrix K(s) (Rosenbrock (1970), Patel and Munro (1982)), then the stability and time domain behavior of the system can be inferred from the diagonal elements of A rational p × p matrix Q(s) is row diagonal dominant on the Nyquist D-contour if Column diagonal dominance is similarly defined by The row diagonal dominance of a system can be determined graphically by superimposing the row dominance Gershgorin circles on the diagonal terms of the direct-system Nyquist array, that is, for each value of frequency  k a circle of radius k a circle of radius is drawn with the center on the diagonal element qii (s) evaluated at s=j k. A similar test for column dominance can be constructed if circles of radius k. A similar test for column dominance can be constructed if circles of radius 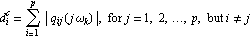 are drawn with centers on the diagonal element qii (s) evaluated at s=j k.
A system is row (column) diagonal dominant over the bandwidth of interest, if none of the bands generated by the Gershgorin circles superimposed on the diagonal terms of the Nyquist array enclose the origin of the associated diagonal element plot.
If a system is row, or column, diagonal dominant then the stability of the multivariable system can be determined by applying the Nyquist stability theorem (Rosenbrock (1970), Patel and Munro (1982)) to the bands generated by the Gershgorin circles, with respect to the individual loop critical points at {-1/ki, 0}, where ki is the additional forward path gain introduced in loop i. For unity feedback in any loop, the critical point is the familiar point {-1, 0}.
Diagonal dominance is also defined for the inverse system k.
A system is row (column) diagonal dominant over the bandwidth of interest, if none of the bands generated by the Gershgorin circles superimposed on the diagonal terms of the Nyquist array enclose the origin of the associated diagonal element plot.
If a system is row, or column, diagonal dominant then the stability of the multivariable system can be determined by applying the Nyquist stability theorem (Rosenbrock (1970), Patel and Munro (1982)) to the bands generated by the Gershgorin circles, with respect to the individual loop critical points at {-1/ki, 0}, where ki is the additional forward path gain introduced in loop i. For unity feedback in any loop, the critical point is the familiar point {-1, 0}.
Diagonal dominance is also defined for the inverse system  and and  , where , where 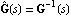 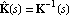 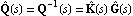 For inverse systems, row diagonal dominance is determined graphically by superimposing the Gershgorin row dominance circles on the diagonal elements of the inverse-system Nyquist array, that is, for each value of frequency  k a circle of radius k a circle of radius is drawn with center on the diagonal element 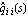 evaluated at s=j evaluated at s=j k. A similar test for column dominance can be constructed if circles of radius k. A similar test for column dominance can be constructed if circles of radius are drawn with center on the diagonal element 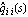 evaluated at s=j evaluated at s=j k. k. For a system with input compensator K(s) = Kp(s)Kd(s), where Kp(s) is a precompensator matrix and Kd(s) is a diagonal matrix of single-loop tuning compensators, and F is a diagonal constant matrix in the feedback path, the resulting closed-loop system transfer-function matrix H(s) is given by where The corresponding relationship for the inverse-system 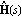 is much simpler, namely, is much simpler, namely, This latter relationship has the property that once the additional loop gains fi have been chosen to define the critical points {-fi, 0} for each feedback loop, the interaction present in loop i, when this loop is open but all other feedback loops are closed, can be assessed by generating the Ostrowski circles (Ostrowski (1952)), which are reduced versions of the Gershgorin circles shrunk by the factor where the Ostrowski circles have radii defined in terms of the corresponding Gershgorin circles as You should note that the Ostrowski circles, as defined here, are not generally used when working with the direct system, as the Gershgorin circles may no longer give the outer bound on the Ostrowski circles, that is, the value that the Ostrowski circles assume when the gains in the loops that are closed are not zero. The inverse of a proper, or strictly proper, nonsingular and invertible system is often a much more complicated mathematical form that does not convey any new information. To avoid computing the explicit representation of an inverse system, you can use the inert wrapper InverseSystem, which preserves the system in an unevaluated form. You can further apply the function Normal to explicitly evaluate such systems. Since most of the functions described in this chapter require the transfer-function matrix form of the inverse system concerned, which is usually improper, and since state-space models and system matrix models are not defined for improper systems, the function Normal returns inverse systems in TransferFunction form. | InverseSystem[system] | an inert wrapper that denotes the inverse of object system |
Representing inverse systems. Make sure the application is loaded. Here is a two-input, two-output transfer-function model of a system. | Out[3]= | 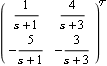 |
This is an unevaluated form of the inverse system. | Out[5]= | 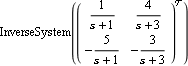 |
This is the explicit form of the inverse system, which is improper. | Out[7]= | 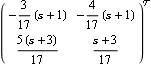 |
This is a state-space realization of the original transfer-function system. | Out[9]= | 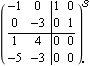 |
Applying the InverseSystem wrapper to the model yields an unevaluated result. | Out[11]= | 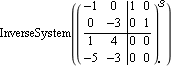 |
The inverse system is improper and is returned in transfer-function form. | Out[13]= | 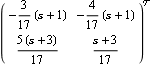 |
In fact, a state-space realization of this system cannot be constructed. | Out[15]= | 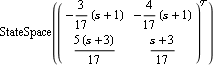 |
|