| FunctionallyControllable[system] |
| | test if the system is functionally controllable |
| LeftHalfPlaneControllable[system] |
|
| | test if the system is functionally controllable and also has no right half-plane transmission zeros |
Testing functional controllability. Make sure the application is loaded. Here is a transfer-function object describing a system with two inputs and two outputs. | Out[3]= | 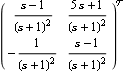 |
This is its McMillan form. | Out[5]= | 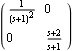 |
Despite the right half-plane zeros at s = +1 in both of the diagonal elements of the original transfer-function matrix, the system is both functionally controllable and left half-plane controllable. | Out[7]= | 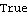 |
| Out[9]= | 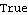 |
Here is another transfer-function object, describing a system with two inputs and three outputs. | Out[11]= | 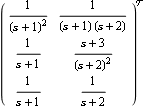 |
The corresponding state-space system is completely controllable and is also output controllable. | Out[13]= | 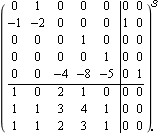 |
| Out[15]= |  |
| Out[17]= |  |
However, since this system has more outputs than inputs, it is not functionally controllable. | Out[19]= |  |
Here is the transpose of this system, which now has three inputs and two outputs. | Out[21]= | 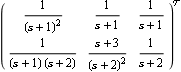 |
Here are all the minors of order 2. | Out[23]= | 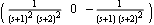 |
Since there is at least one nonzero 2 × 2 minor, this system is functionally controllable. | Out[25]= |  |
Here is yet another system that is functionally controllable. | Out[27]= | 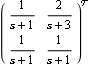 |
| Out[29]= |  |
The system has a zero at s = +1 in the McMillan form of the transfer-function model, and so it is not left half-plane controllable. | Out[31]= | 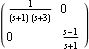 |
| Out[33]= |  |
In fact, it is not possible to set up two simultaneous high-gain feedback loops, that is, loops with a gain > 10, say, around this apparently simple multivariable system, and maintain stability (see Section 4.1.4). |