|
SystemMatrix[var, t, u, v] creates a system matrix from the polynomial matrices T, U, and V, in the variable var, assuming a zero matrix W. SystemMatrix[var, t, u, v, w] uses a possibly nonzero matrix W. Following the convention for TransferFunction, SystemMatrix (and LeftMatrixFraction and RightMatrixFraction introduced later in this chapter), let you omit the variable var. If the variable is not present, the formal variable # is used. Regardless of the way you enter it, a SystemMatrix object keeps the component matrices in a block matrix {{T, U}, {-V, W}}. If the latter needs to be constructed from a sequence of matrices T, U, V (and optionally W), SystemMatrix automatically adjusts the dimensions of T, U, and V to ensure that these matrices meet the definition of a system matrix. SystemMatrix, and other control objects in this chapter, also follow the convention for TransferFunction in using the variables 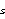 and  (the Mathematica characters \[ScriptS] and \[ScriptZ]) to represent the complex variables of the Laplace-transform domain and z-transform domain in TraditionalForm. You can use ToDiscreteTime and ToContinuousTime to convert the new objects to and from discrete-time form, as discussed later in Section 3.5. | | create a system matrix from the polynomial matrices t, u, and v, in the formal variable # |
| SystemMatrix[var, t, u, v] |
| | create a system matrix from the polynomial matrices t, u, and v, in the variable var |
| SystemMatrix[var, t, u, v, w] |
| | create a system matrix from the polynomial matrices t, u, v, and w, in the variable var |
| SystemMatrix[{{t, u}, {-v, w}}] |
| | a system matrix comprising the polynomial matrices t, u, -v, and w, in the formal variable # |
| SystemMatrix[var, {{t, u}, {-v, w}}] |
| | a system matrix representation in the variable var |
System matrix data structure. Make sure the application is loaded. Here are some polynomial matrices T, U, and V. This is the resulting SystemMatrix object. If you do not supply matrix W, it is assumed to be a zero matrix. | Out[6]= |  |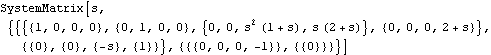
This is the same matrix in TraditionalForm, the format customarily used in this guide. | Out[8]= |  |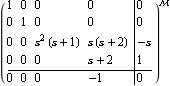
This output format shows one matrix that contains the polynomial system matrix model, where the upper-left partition contains the matrix T, the upper-right partition contains the matrix U, the lower-left partition contains the matrix -V, and the lower-right partition contains the matrix W. The superscript 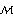 indicates that this one matrix is a SystemMatrix object containing the entire system data. Note that SystemMatrix automatically inflated the dimensions of the matrices by adding two system variables to construct a valid system matrix object.
Similarly to TransferFunction, a SystemMatrix object acts as a function so that you can apply it to a variable to extract the underlying matrices in that variable. This produces a block matrix,  DisplayForm, in the variable s. | Out[10]= |  |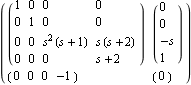
This combines the matrix components into a single matrix. | Out[12]= |  |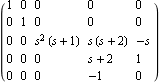
As a shortcut, you may sometimes find it useful to construct a SystemMatrix object directly by providing the component matrices in the block matrix form {{t, u}, {-v, w}}. In that case, you should remember to supply the matrix V with the negative sign and make sure that matrix T is of appropriate dimensions, as entering a system matrix in this form circumvents the normal mechanism that ensures that matrix T has enough degrees of freedom. This reconstructs the SystemMatrix object from the component matrices. | Out[14]= |  |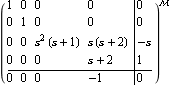
|
