3.3.4 Minimizing the Dimensions of a System Matrix Object

SystemEquivalentReduce is a function that applies system equivalence transformations to a SystemMatrix object in order to determine the smallest dimensions of the T, U, -V, and W matrices, necessary for the system to meet the requirement that the dimension of the matrix T is greater than or equal to the degree of |T(s)|.

System equivalence operations (Rosenbrock (1970), Patel and Munro (1982)) are operations that can be applied (in particular) to system matrices in polynomial form. The function SystemEquivalentReduce makes use of two of these transformations, as follows:

1. Interchange any two of the first r rows or columns of the system matrix that contain only a single nonzero constant, where r is the size of matrix T.
2. Delete a row, and the corresponding column, of the system matrix that contains only a single nonzero constant.

For example, a system matrix that has been manipulated using these operations into the form

where D_k is a diagonal matrix of k constants and P(s) is a system matrix satisfying the definition given in Eq. (3.7), can be further simplified to

by deleting the first k rows and columns, where P_{1}(s) and P_{2}(s) both have the same order and generate the same transfer-function matrix G(s).

Simplifying the system matrix object.

Make sure the application is loaded.

In[1]:=

Here is a system matrix with the dimension r of the matrix T equal to 6.

In[2]:=

I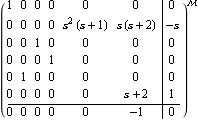n[3]:=

In[4]:=

In[5]:=

Out[6]=

Since the degree of |T(s)| is 4, a lower-dimension system matrix may exist.

In[7]:=

O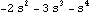ut[8]=

This finds a lower-dimension system matrix.

In[9]:=

Ou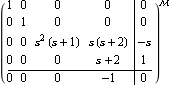t[10]=

Both of these system matrices yield the same transfer function.

In[11]:=

O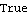ut[12]=