Similarly, RightMatrixFraction creates a right matrix-fraction model of a system from the numerator and denominator matrices, or another control object. | RightMatrixFraction[n, d] |
| | create a right matrix fraction with numerator matrix n, and denominator matrix d, in the formal variable # |
| RightMatrixFraction[var, n, d] |
| | create a right matrix fraction with numerator matrix n, and denominator matrix d, in the formal variable var |
Right matrix-fraction data structure. Make sure the application is loaded. Here is the data describing the matrices N(s) and D(s) of a right matrix-fraction model of a system. | Out[3]= |  |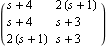
| Out[5]= |  |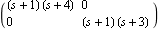
RightMatrixFraction keeps its component matrices unchanged. | Out[7]= |  |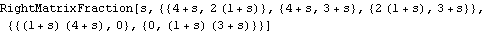
This is the TraditionalForm representation of the same object. | Out[9]= |  |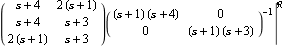
This output format shows one object that consists of two matrices. The first contains the numerator matrix N(s), and the second contains the inverse of the denominator matrix D(s). The |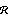 indicates that these two matrices constitute a RightMatrixFraction object.
Similarly to other polynomial control objects, you can apply the RightMatrixFraction object to a variable to extract the underlying matrices in that variable.
This produces a list of matrices N and D in the variable s. | Out[11]= |  |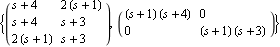
A right matrix-fraction model can also be created from an existing system in transfer-function, zero-pole-gain, state-space, system matrix, or left matrix-fraction form. These conversions are carried out in a similar way to those described for the left matrix-fraction case. | RightMatrixFraction[system] |
| | create a right matrix-fraction object of a system, in the formal variable # |
| RightMatrixFraction[var, system] |
| | create a right matrix-fraction object in the specified variable var |
Right matrix-fraction data structure for converting from other system forms. Here is a TransferFunction object representing a system with two inputs and three outputs. | Out[13]= |  |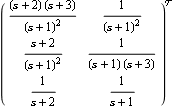
This is the corresponding StateSpace object. | Out[15]= |  |
This constructs a right matrix-fraction object. Since no formal variable is supplied, the result is obtained in the pure function form, that is, in the variable #. | Out[17]= |  |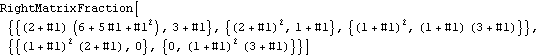
You can also construct a RightMatrixFraction object in the variable of your choice. | Out[19]= |  |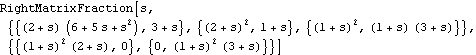
A RightMatrixFraction object can equally be generated directly from a LeftMatrixFraction object. Here is a LeftMatrixFraction corresponding to the transfer-function object. | Out[21]= |  |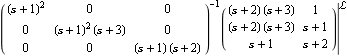
This is the RightMatrixFraction determined directly from the LeftMatrixFraction object. | Out[23]= |  |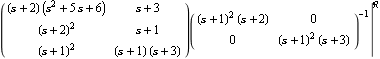
This shows the correspondence between the right matrix-fraction model and the system matrix model, when the default value of TargetForm -> Automatic is used. | Out[25]= |  |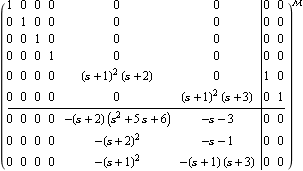
|
