The matrix greatest common divisors of the numerator and denominator matrices of matrix-fraction models are useful for generating LeftMatrixFraction and RightMatrixFraction objects with the least possible dynamic order. The functions LeftGCDDecomposition and RightGCDDecomposition find the left and right matrix GCDs L(s) and R(s), respectively, of a pair of polynomial matrices, and the corresponding least-order representations 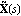 , , 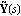 and and 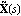 , , 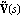 according to Eq. (4.18) and Eq. (4.23). according to Eq. (4.18) and Eq. (4.23). Both functions return a list of matrices. LeftGCDDecomposition returns the list {L(s), 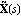 , , 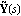 } and RightGCDDecomposition returns the list {R(s), } and RightGCDDecomposition returns the list {R(s), 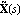 , , 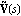 }. }. | LeftGCDDecomposition[m{1}, m{2}, var] |
| | find the left greatest common divisor decomposition of the two polynomial matrices m{1} and m{2}, in the variable var |
| RightGCDDecomposition[m{1}, m{2}, var] |
|
| | find the right greatest common divisor decomposition of the two polynomial matrices m{1} and m{2}, in the variable var |
The LeftGCDDecomposition and RightGCDDecomposition functions. Make sure the application is loaded. Here is a left matrix-fraction model. | Out[3]= | 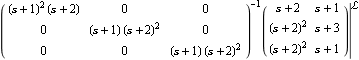 |
This is not a least-order object. | Out[5]= |  |
This extracts the polynomial matrices D(s) and N(s), by applying the LeftMatrixFraction object to the variable s. These are the matrices. | Out[8]= | 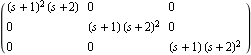 |
| Out[10]= | 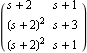 |
The order of this matrix fraction is 9, as given by the degree of the determinant |D(s)|. | Out[12]= | 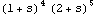 |
This finds the left matrix GCD and the reduced-order matrices Dr(s) and Nr(s). | Out[15]= | 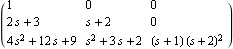 |
| Out[17]= | 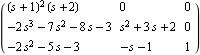 |
| Out[19]= | 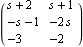 |
The order of the reduced matrix fraction is 5, as given by the degree of the determinant |Dr(s)|. | Out[21]= | 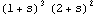 |
The order of the left matrix GCD is 4, as given by the degree of the determinant |L(s)|. | Out[23]= | 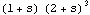 |
Applying the function SmithForm to the block matrix [D(s) N(s)] confirms the common polynomial factors of the pair of matrices D(s) and N(s) of the original LeftMatrixFraction object. | Out[25]= | 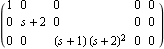 |
You can also obtain the reduced-order form of the LeftMatrixFraction object directly using the function LeastOrderSystem, introduced later in Section 4.4.3. | Out[27]= | 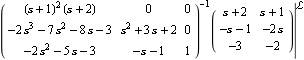 |
Here is a RightMatrixFraction object. | Out[29]= | 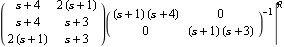 |
This is a least-order right matrix fraction. | Out[31]= | 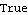 |
This extracts the polynomial matrices N(s) and D(s), by applying RightMatrixFraction to the variable s. This constructs a block matrix  . . | Out[34]= | 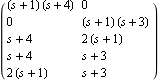 |
Since the Smith form of the block matrix has a leading identity matrix, the matrices N(s) and D(s) of the right matrix fraction are coprime, or least order. | Out[36]= |  |
In this case, the function LeastOrderSystem returns the original system. | Out[38]= | 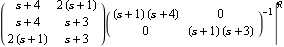 |
|