Legacy Documentation

Polynomial Control Systems (2014)

This is documentation for an obsolete product.
Current products and services

Linear System Analysis / Decoupling Zeros /
Previous section-----Next section

4.4.3 Creating Least-Order Systems

The function LeastOrderSystem can be used with the control objects SystemMatrix, LeftMatrixFraction, and RightMatrixFraction to create least-order systems, that is, systems with no decoupling zeros. This function can also be applied to a system matrix in state-space form.

Creating a least-order system.

Make sure the application is loaded.

In[1]:=

Here is a SystemMatrix of a 5th-order system with two inputs and three outputs.

In[2]:=
O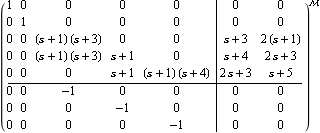ut[3]=

Since there is an input decoupling zero at s = -1, the system matrix does not represent a least-order system.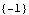

In[4]:=
Out[5]=
In[6]:=
Out[7]=

This creates a least-order form of the system.

In[8]:=
O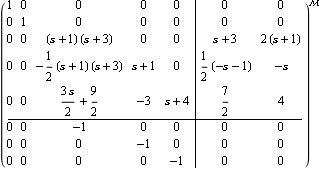ut[9]=

Since the matrix T(s) in both the original and the reduced-order system matrix models is lower triangular, it is easy to see that the order of the system matrix, given by the order of the determinant of T(s), has now been reduced from 5 to 4.

Indeed, this least-order system does not have any input or output decoupling zeros.

In[10]:=
O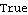ut[11]=

Here is a system matrix in state-space form that is observable but not controllable.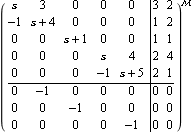

In[12]:=
Out[13]=
In[14]:=
Out[15]=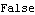
In[16]:=
Out[17]=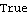

This creates a system matrix in state-space form that is both controllable and observable.

In[18]:=
Out[19]=

Control System Professional functions Controllable and Observable, normally used with StateSpace objects, can also now be applied directly to SystemMatrix objects, and to LeftMatrixFraction and RightMatrixFraction objects.

The extended Controllable and Observable functions.

This confirms that the system is both controllable and observable.

In[20]:=
Out[21]=

Here is a left matrix-fraction object of a system with two inputs and three outputs.

In[22]:=
Out[23]=

This is not a least-order system, since the denominator matrix D(s) and the numerator matrix N(s) are not left coprime.

In[24]:=
Out[25]=

This is a least-order version of the matrix-fraction system.

In[26]:=
O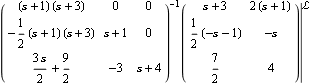ut[27]=

You can apply the functions Controllable and Observable directly to this object, without having to create a corresponding state-space form, to confirm that this is a least-order system.

In[28]:=
Out[29]=