Section 8.7 of Control System Professional describes how there can be an infinite number of equivalent realizations of a state-space model of a physical system, and shows how these are all related by a similarity transformation. Here, the application of a similarity transform to a system matrix object is introduced.
If P(s) is a system matrix representation of an original system in state-space form S = {A, B, C, D} and P1(s) is a system matrix representation of the transformed system description S1={A1, B1, C1, D}, then S and S1are related by the system similarity transformation where the subscripts q and p refer to the number of system outputs and inputs, respectively. The existing function SimilarityTransform, which is normally used with StateSpace objects, can also now be used with SystemMatrix objects in state-space, or polynomial, form. The analog of Eq. (4.40) for the case of a system matrix in polynomial form is | SimilarityTransform[system, matrix] |
| | transform the object system with the matrix matrix |
Finding the similarity transformation. Make sure the application is loaded. Here is a state-space object. | Out[3]= | 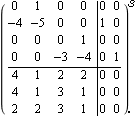 |
This is a nonsingular transformation matrix H consisting of the eigenvectors of the matrix A in the state-space description. | Out[5]= | 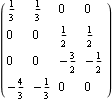 |
This is the resulting diagonal form of the state-space object, under this transformation. | Out[7]= | 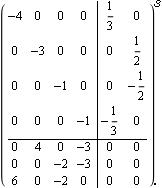 |
This is the system matrix object corresponding to the original system, in the variable s. | Out[9]= | 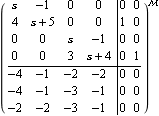 |
Here is the resulting diagonal form of the system matrix representation, under the same transformation. | Out[11]= | 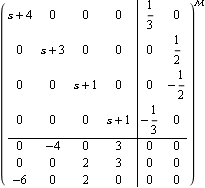 |
Here is a transfer-function object. | Out[13]= | 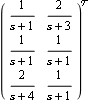 |
This is the corresponding system matrix object. | Out[15]= | 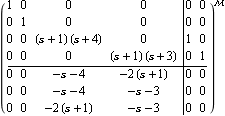 |
Here is a simple constant transformation matrix. | Out[17]= |  |
This is the resulting transformed system matrix representation. | Out[19]= | 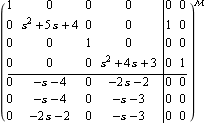 |
The transformed system matrix generates the original transfer-function object. | Out[21]= | 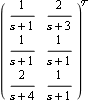 |
|