This chapter introduces the design of controllers for multivariable systems using frequency domain techniques. It is the presence of interaction between the inputs and outputs in such systems that usually makes it impossible to directly apply the well-established tools for the design of single-input, single-output systems. However, if a precompensator can be constructed such that the interaction in the multivariable system can be sufficiently reduced, or removed (this is known as decoupling), then the established single-input, single-output system tools can be effectively employed to design the remaining loop-tuning compensators. Figure 5.1 shows this for a two-input, two-output multivariable system, where Kp(s) is a multivariable precompensator designed to reduce the interaction in the system, and k1(s) and k2(s) are two single-loop tuning compensators. 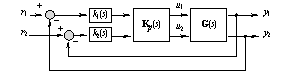
Figure 5.1. A two-input, two-output system feedback configuration. Systems with more outputs than inputs are not functionally controllable (see Section 4.2), and it is not possible to independently control all the outputs. However, for systems with more inputs than outputs, the system may be functionally controllable using only a subset of the inputs, and for systems with the same number of inputs and outputs, the system is functionally controllable if the determinant of the corresponding transfer-function matrix is not identically zero. In these latter cases, the relative gain array can be useful in helping the designer to select the best inputs for control. Several analysis and design tools that may considerably reduce the interaction in a multivariable system are presented in the following sections. These include the application of the relative gain array, the Nyquist array approach, the characteristic locus method, the Perron-Frobenius scaling procedure, and other methods. |