The Smith form of a polynomial matrix, left matrix-fraction, right matrix-fraction, or system matrix object, can be determined by using the function SmithForm. | SmithForm[system] | find the Smith form of a system matrix, left matrix-fraction, or right matrix-fraction system | | SmithForm[m, var] | find the Smith form of the polynomial matrix m in the variable var |
Finding the Smith form. Make sure the application is loaded. Here is a square polynomial matrix in the variable s. | Out[3]= |  |
This is the Smith form of this polynomial matrix. | Out[5]= |  |
Here is a system matrix in the variable s. | Out[7]= |  |
This is the Smith form of this system matrix. | Out[9]= |  |
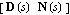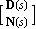When analyzing matrix-fraction objects, the designer is often interested in the Smith form of the combination of the numerator and denominator matrices, namely, the composite matrix  for a left matrix fraction or the composite matrix  for a right matrix fraction, as explained later in Section 4.3 on coprimeness. Here is a left matrix-fraction model of a system with two inputs and three outputs. | Out[11]= |  |
This is the Smith form of the matrix pair [D(s) N(s)] of this left matrix fraction. | Out[13]= |  |
Since the resulting Smith form is not equal to [I3 0], the two matrices D(s) and N(s) describing the left matrix-fraction object are not relatively left prime. This means that a lower-order model of the left matrix fraction exists that will generate the same transfer-function model, as explained later in Section 4.3. |
