The roots of the polynomials  i(s) on the diagonal of the Smith form of a system matrix, in either state-space or polynomial form, are called the invariant zeros of the system, since these do not change when either constant state or constant output feedback is applied to the system. The function InvariantZeros can be used to determine the invariant zeros of a state-space, transfer-function, system matrix, or left or right matrix-fraction model. | InvariantZeros[system] | determine the invariant zeros of the object system |
Determining the invariant zeros of a system. Make sure the application is loaded. Here is a transfer-function object. | Out[3]= |  |
These are its invariant zeros. | Out[5]= |  |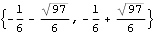
InvariantZeros finds the roots of the diagonal elements of the Smith form of the corresponding system matrix. This is a system matrix. | Out[7]= |  |
This is its Smith form. | Out[9]= |  |
These are the roots of the last polynomial on the diagonal. | Out[11]= |  |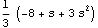
| Out[13]= |  |
Of course, you can obtain the same zeros from the system matrix representation. | Out[15]= |  |
Here is a state-space model for this system. | Out[17]= |  |
These are its eigenvalues. | Out[19]= |  |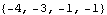
This is a possible state feedback gain matrix. | Out[21]= |  |
This forms the closed-loop system. | Out[23]= |  |
These are the new eigenvalues. | Out[25]= |  |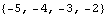
However, the invariant zeros are unchanged by this feedback. | Out[27]= |  |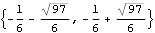
|
