The McMillan form of a rational polynomial matrix, as illustrated earlier in Example 4.1, can be determined by using the function McMillanForm. | McMillanForm[tf] | find the McMillan form of the TransferFunction object tf | | McMillanForm[m, var]
| find the McMillan form of the rational polynomial matrix m in the variable var |
Finding the McMillan form. Make sure the application is loaded. Here is a transfer-function object. | Out[3]= | 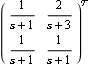 |
This is its McMillan form. | Out[5]= |  |
Note that although the individual transfer-function elements of the TransferFunction object have no numerator dynamics, the McMillan form reveals that the system has a multivariable zero at s=+1. The significance of this zero, which is known as a transmission zero, is explained in Section 4.1.4. You can also apply the function McMillanForm directly to a rational polynomial matrix. | Out[7]= | 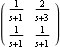 |
| Out[9]= | 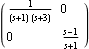 |
The McMillan degree of a transfer-function matrix is the total number of poles in the diagonal elements of the matrix in its McMillan form. This number determines the order of any minimal state-space realization of the transfer-function matrix or the minimal order of coprime matrix-fraction models. | McMillanDegree[tf] | determine the McMillan degree of the TransferFunction object tf | | McMillanDegree[m, var]
| determine the McMillan degree of the rational polynomial matrix m in the variable var |
Determining the McMillan degree. Here is the McMillan degree of the preceding transfer-function object. | Out[11]= | 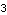 |
Since the McMillan degree is three, a minimal state-space realization of this transfer-function matrix will be of order three, even though there are four poles in the elements of the transfer-function matrix. Here is a controllable state-space realization. | Out[13]= | 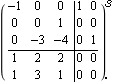 |
This third-order realization is both controllable and observable and, therefore, minimal. | Out[15]= |  |
|