Any set of linear differential equations, relating the system variables xi(t) and their rth-order derivatives drxi(t)/dtr to the system outputs yj(t) and inputs uk(t), can be reduced to an equivalent set of first-order differential equations by the introduction of a set of additional variables (Rosenbrock (1970), Patel and Munro (1982)). This latter set of equations along with any algebraic equations can then be written as where x(t) is an n × 1 vector of (state) variables, u(t) is a p × 1 vector of input functions, and y(t) is a q × 1 vector of outputs. The matrices A, B, C, and D have constant coefficients and are of dimension n × n, n × p, q × n, and q × p, respectively. For a simple fourth-order mass-spring system shown in Figure 3.1, the linearized equations of motion about an equilibrium point are where the springs are characterized by spring rates r1 and r2 and the masses are represented by mass elements m1 and m2. The system is subjected to an input force u applied to mass m1. The output of interest is the displacement y = x2 of the mass m2.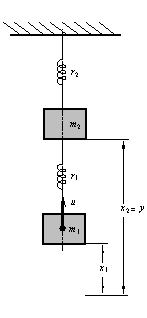 
Figure 3.1. Simple mass-spring system. By introducing additional variables x3 and x4 according to these equations can be written in state-space form as The state-space description of this system StateSpace[a, b, c, d] consists of the StateSpace object wrapper and the corresponding matrices. Make sure the application is loaded. This is a state-space representation of the system. | Out[3]= |  |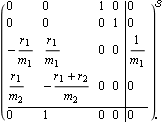
The output format shows one matrix that contains the state-space system model, where the upper-left partition contains the matrix A, the upper-right partition contains the matrix B, the lower-left partition contains the matrix C, and the lower-right partition contains the matrix D. The superscripted letter 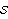 identifies the StateSpace object, while the small subscripted bullet character denotes the continuous-time domain. |
