When creating a system matrix model from an existing TransferFunction, or ZeroPoleGain object, you can choose between one of two forms for the resulting SystemMatrix by using the SystemMatrix option TargetForm. For TargetForm  RightFraction, the transfer-function matrix G(s), of a system with q outputs and p inputs, is first expressed as where DR(s) is a p × p diagonal matrix containing the least common denominators of each of the p columns of G(s), and NR(s) is a q × p matrix containing the resulting numerator terms. The system matrix is then constructed as where Ir-n is the identity matrix of dimensions r-n, Ipis the identity matrix of dimensions p, and (as before) r is the dimension of the matrix where n is the order of the determinant |DR(s)|. Essentially, this form of the resulting system matrix contains all the numerator dynamics of G(s) in the matrix V(s). When TargetForm LeftFraction is used, the transfer-function matrix G(s) is expressed as where DL(s) is a q × q diagonal matrix containing the least common denominators of each of the q rows of G(s), and NL(s) is a q × p matrix containing the corresponding numerator terms. The system matrix is then constructed as where Iq is the identity matrix of dimensions q, and r is the dimension of the matrix where n is the order of |D{L}(s)|. Essentially, this form of the resulting system matrix contains all the numerator dynamics of G(s) in the matrix U(s). The default value of the option TargetForm is Automatic. When creating a system matrix from a TransferFunction or ZeroPoleGain object, this corresponds to TargetForm RightFraction. For StateSpace, LeftMatrixFraction, and RightMatrixFraction objects, the Automatic setting brings about the state-space, left-fraction, and right-fraction forms, respectively. Automatic is the only available choice for converting StateSpace objects to SystemMatrix form. | option name | default value | | | TargetForm | Automatic | form to use in the SystemMatrix object |
The TargetForm option. Make sure the application is loaded. Consider the transfer-function matrix model of a multivariable system, with two inputs and two outputs. | Out[3]= |  |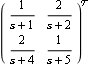
By default, SystemMatrix constructs a system matrix object in right-fraction form. | Out[5]= |  |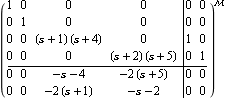
This is the left-fraction form of the same transfer-function object. | Out[7]= |  |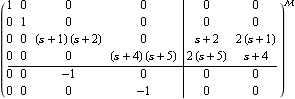
Both of the preceding system matrices yield the same transfer-function object. | Out[9]= |  |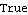
|
