Any of the existing control objects, StateSpace, TransferFunction, and ZeroPoleGain, and the new objects LeftMatrixFraction (described in Section 3.4.1), and RightMatrixFraction (described in Section 3.4.2) can be converted to a SystemMatrix form. In the case of StateSpace objects, the resulting SystemMatrix has the special form shown previously in Eq. (3.8), namely | SystemMatrix[system] | create a system matrix representation of the object system | | SystemMatrix[var, system] | create a system matrix representation of the object system, in the formal parameter var |
Conversion of control objects to system matrix form. Make sure the application is loaded. Here is a simple third-order state-space system, with one input and two outputs. | Out[3]= | 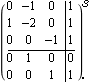 |
This finds its corresponding system matrix form, in the variable s. | Out[5]= | 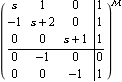 |
Here is the transfer-function matrix model of another multivariable system, with two inputs and three outputs. | Out[7]= | 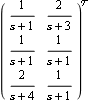 |
This creates its corresponding system matrix. | Out[9]= | 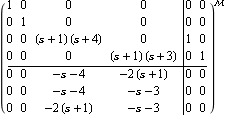 |
Conversely, you can readily find a state-space realization, transfer-function matrix, and other representations of a SystemMatrix object by applying the StateSpace, TransferFunction, and other "active wrappers". This recovers the original TransferFunction object. | Out[11]= | 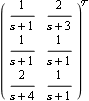 |
This finds a state-space realization of the system matrix object. The result is a fourth-order state-space system. | Out[13]= | 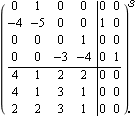 |
|