6. Pole Assignment and State Reconstruction

Pole assignment as a design technique is introduced in Section 9.1 of Control System Professional, but is briefly reviewed here for completeness. Given an n^"th"-order system in state-space form

then with the state-feedback control u= r-Kx, where r is the reference input vector for the closed-loop system, the closed-loop system's poles, that is, the eigenvalues of the matrix A-BK, assume new values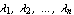

Various algorithms have been developed by different researchers to determine the matrix K that yields the desired closed-loop pole locations _i. In this chapter, additional state-feedback methods are presented that each have advantages and disadvantages depending on the problem concerned. Two dyadic algorithms, that is, algorithms that produce state-feedback compensators created as the outer product of two vectors and hence only have rank 1, are presented. One is known as the spectral approach and the other is known as the mapping approach. Both of these will generate the same results as Ackermann's method, since the state-feedback gains developed for a single-input system, to meet a given pole assignment requirement, are unique. However, it is also known that the resulting closed-loop system will not have good disturbance rejection properties, with these approaches. A third algorithm, known as the full-rank approach, generates a maximum rank compensator for a given multi-input system. The resulting closed-loop system has improved disturbance rejection properties with this approach. In addition, the gain values needed to achieve a desired closed-loop pole specification are often considerably lower in value with this algorithm than those obtained when using the dyadic algorithms. This has the additional advantage of possibly avoiding actuator saturation, due to the reduced signal levels involved.

As stated in Section 9.1 of Control System Professional, feedback design is prone to significant numerical errors, especially for high-order, or weakly controllable, systems. The algorithms presented here provide additional alternative ways of designing the required state feedback. You can use the option Method with the function StateFeedbackGains to select the desired algorithm.

The dyadic state-feedback algorithms may be used with both single-input and multi-input systems. For any multi-input system {A, B} that is completely controllable, a column matrix BF can always be determined (Wonham (1967)) such that the single-input system {A, BF} is also completely controllable. The column matrix F is known as the fan-in vector, since it distributes the scalar feedback signal across the original system input vectors. The option ControlInput All can be used in such cases to find the "best" fan-in vector F using the condition number of the corresponding controllability matrix as a criterion. Using this latter test criterion, it may turn out that the best fan-in vector is not some combination of the input vectors, but is simply one of the original input vectors. It is also possible to specify the fan-in vector to be used explicitly, by setting ControlInput {f₁, f₂, ...}, where the f_i are the weightings to be applied to the inputs to be used. When ControlInput Automatic, the best single input is determined such that the resulting controllability matrix has the smallest condition number. Finally, ControlInput n specifies that the n^th input is to be used.

Option specific to the dyadic state-feedback and output-feedback algorithms.

The pole assignment problem using constant and dynamic output feedback is treated in Section 6.6.