This dyadic output feedback algorithm can be considered as a polynomial-based, or frequency-domain, approach. Given an n"th"-order linear system in state-space form with q outputs and p inputs and the corresponding transfer-function matrix G(s), using the output feedback law u(s)=r(s)-K(s)y(s), where r is the reference input vector for the closed-loop system, and K(s) is in general a dynamic compensator of degree r, as shown in Figure 6.2, the closed-loop system's poles, that is the poles of the matrix can be made to assume new values  {1},{2},...,n{+}r.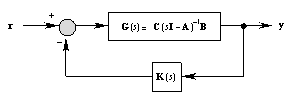 
Figure 6.2. System with output-feedback pole assignment compensator. The required compensator can be considered as the product of a column matrix F and a row matrix MT(s), that is, where F is a column matrix of constants chosen such that the resulting system is completely controllable, that is, the system {A, BF} is completely controllable. Let g(s) be expressed as where is the characteristic polynomial of G(s), and the numerator terms are Let MT(s) have the form where is the characteristic polynomial of MT(s), and the numerator terms are The resulting closed-loop system characteristic polynomial  d(s) (Chen and Hsu (1971)), is given by the relationship where If the degree of the compensator is chosen as where  c and o are the controllability index (see Section 6.4.1) and observability index (see Section 6.4.2) for the system, respectively, Eq. (6.24) can be solved for the parameters  i and  i that define the compensator. If the system being considered has a matrix C that is equal to In, where n is the number of states, or the matrix C is invertible, then the degree of the compensator required is zero. If C = In, the algorithm generates the constant state-feedback compensator. The function OutputFeedbackCompensator with the option Method  Dyadic implements this algorithm. | OutputFeedbackCompensator[system, {{1}, ..., n{+}r}, Method -> Dyadic] |
| | determine a dyadic output feedback compensator of degree r that assigns the poles of the closed-loop system to 1, ..., n+r |
Output feedback compensator function, using dyadic feedback. The compensator generated by this output feedback algorithm is generally of lower order than those generated using state feedback with an observer of order n-q, or a full-state estimator with order n. Make sure the application is loaded. Consider a two-input, two-output state-space system. | Out[3]= |  |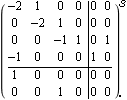
These are the open-loop system eigenvalues. | Out[5]= |  |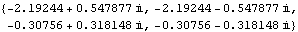
These are the controllability and observability indices of the system. | Out[7]= |  |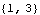
| Out[9]= |  |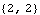
Since the system controllability index is 3 and the system observability index is 2, a feedback compensator of order 1 can be designed to reassign the system poles to new values. This can be confirmed by using the function OutputFeedbackCompensatorDegree with the option Method Dyadic. | OutputFeedbackCompensatorDegree[system, Method -> Dyadic] |
| | determine the degree of the dyadic output feedback compensator needed to assign the poles of system to arbitrary new values, subject to complex pairing |
Output feedback compensator degree function, used with dyadic output feedback. This confirms the degree of the desired dyadic output feedback compensator for this system. | Out[11]= |  |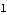
These are the desired closed-loop system poles, including one extra closed-loop pole position at s = -1 for the extra dynamics introduced by the compensator. This is the dynamic compensator of degree 1, needed to assign these closed-loop system poles. | Out[14]= |  |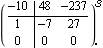
This closes the feedback loops around the system with this compensator, using negative feedback. | Out[16]= |  |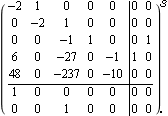
These are the resulting closed-loop system poles. | Out[18]= |  |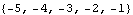
Here is a simulation of the open-loop system, with unit-step functions applied separately to each input.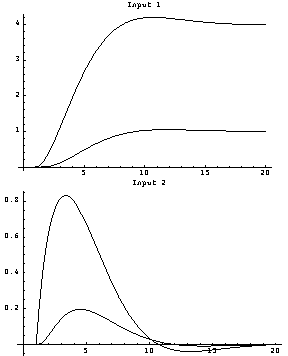 
This shows the closed-loop system behavior, with unit-step functions applied separately to each input, which are now much faster and settle down in a shorter time. The magnitude of the responses is now much smaller due to the feedback.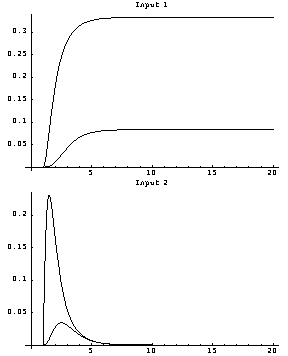 
This is the same state-space system with the matrix C replaced by a unit matrix In, which effectively gives access to all states for state feedback. | Out[24]= |  |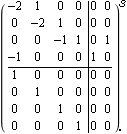
The controllability indices remain the same, but the observability indices have changed. | Out[26]= |  |
| Out[28]= |  |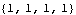
Since the system controllability index is 3 and the system observability index is now 1, r = Min[c-1, o-1] = 0, and a constant dyadic output feedback compensator can be designed to reassign the system poles to new values. These are the desired closed-loop system poles. This is the constant output feedback compensator needed to assign these closed-loop system poles. | Out[31]= |  |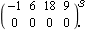
The corresponding compensator determined using state feedback with the mapping algorithm is identical. | Out[33]= |  |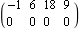
This closes the feedback loops around the system with this compensator, using negative feedback. | Out[35]= |  |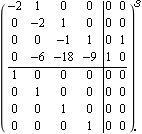
These are the resulting closed-loop system poles. | Out[37]= |  |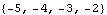
This restores the original output matrix C. | Out[39]= |  |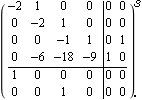
Here is a simulation of the resulting closed-loop system, with unit-step functions applied separately to each input.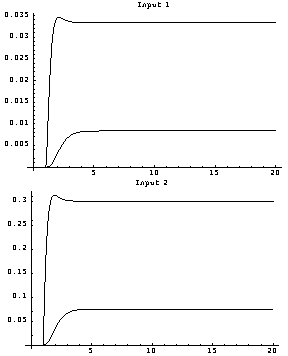 
The closed-loop system responses obtained in this latter case are faster. This is due to the compensator pole having been placed at s=-1 in the dynamic output feedback case. |
