Using the option Method 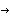 FullRank, the function OutputFeedbackCompensator computes the required full-rank output compensator in a sequence of p steps, where p is the number of inputs, using the algorithm by Söylemez and Munro (2001). If a dynamic compensator is required, then the required dynamics are only introduced in the last step of the algorithm. The degree of the compensator is given by where  . means ceiling, and the  i are determined as where  . means floor. In general, you can specify the poles of the dynamic compensator to be determined, and hence guarantee the internal stability of the system. However, if there are not enough degrees of freedom available in the final step of the algorithm, the poles of the compensator are determined by the algorithm. OutputFeedbackCompensator[system, { 1, ..., n{+}r}, Method -> FullRank] |
| | determine a dynamic feedback compensator of degree r for a single-input, multi-output, or single-output, multi-input, system that assigns the poles of the closed-loop system to 1, ..., n{+}r
|
OutputFeedbackCompensator[system, {{1}, ..., n{+}r}, { 1, ..., r}, Method -> FullRank] |
|
| | determine a dynamic feedback compensator of degree r that assigns the poles of the closed-loop system to 1, ..., n{+}r, using a dynamic compensator with open-loop poles 1, ..., r |
Output feedback compensator function, using full-rank feedback. The degree of a full-rank compensator required for a given system can be determined in advance of using the function OutputFeedbackCompensator, by using the function OutputFeedbackCompensatorDegree, introduced in Section 6.6.1, with the option Method -> FullRank. Make sure the application is loaded. Consider the third-order single-input, single-output state-space system. | Out[3]= |  |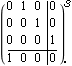
These are the open-loop system eigenvalues. | Out[5]= |  |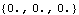
The system is completely controllable and observable. | Out[7]= |  |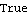
| Out[9]= |  |
Since the system only has 1 input, = {1}, and since the order of the system is n = 3, the degree of the compensator required to relocate the system poles to new values is This confirms the order of the desired compensator. | Out[11]= |  |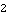
These are the desired closed-loop system poles (including the closed-loop location of the two compensator poles). This is the dynamic compensator of degree 2, needed to assign these closed-loop system poles. Since the system has only one input and only one output, the compensator poles needed to achieve the desired overall closed-loop system poles cannot be specified, and are determined by the algorithm. | Out[14]= |  |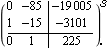
These are the poles of the compensator determined by the algorithm. | Out[16]= |  |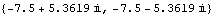
This closes the feedback loop with this compensator, using negative output feedback. | Out[18]= |  |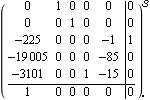
These are the resulting closed-loop system poles. | Out[20]= |  |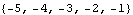
Consider the seventh-order three-input, four-output unstable state-space system. | Out[22]= |  |
These are the open-loop system eigenvalues. | Out[24]= |  |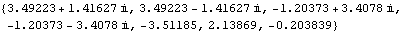
The system is both controllable and observable. | Out[26]= |  |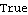
| Out[28]= |  |
Here, i = {1, 2, 4}, and since the order of the system is n = 7, the compensator required to relocate the system poles to new values is constant, since This confirms the order of the desired compensator. | Out[30]= |  |
These are the desired closed-loop poles. This is the resulting constant compensator, needed to assign these closed-loop system poles. | Out[33]= |  |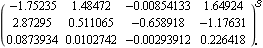
This confirms that the compensator has maximum rank = 3. | Out[35]= |  |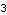
This closes the feedback loop with this compensator, using negative output feedback. These are the resulting closed-loop system poles. | Out[38]= |  |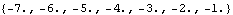
Consider the eighth-order two-input, four-output unstable state-space system. | Out[40]= |  |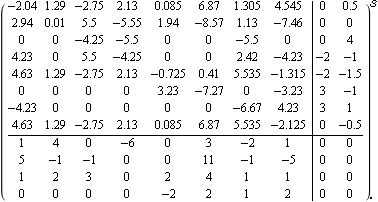
These are the open-loop system eigenvalues. | Out[42]= |  |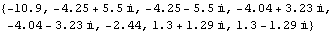
The system is both controllable and observable. | Out[44]= |  |
| Out[46]= |  |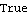
Here, the i = {2, 4}, and since the order of the system is n = 8, the dynamic compensator required to relocate the system poles to new values has degree This is the desired open-loop compensator pole. These are the desired closed-loop system poles (including the closed-loop location of the compensator pole). This is the resulting first-order dynamic compensator needed to assign these closed-loop system poles. | Out[50]= |  |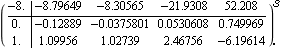
This closes the feedback loops with this compensator, using negative output feedback. These are the resulting closed-loop system poles. | Out[53]= |  |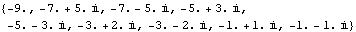
This is the transfer-function form of the compensator. | Out[55]= |  |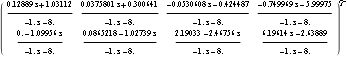
This confirms that the compensator has maximum rank = 2. | Out[57]= |  |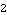
Here is the resulting first-order compensator for the same system, when the open-loop compensator pole is set to s = -6. | Out[61]= |  |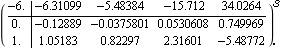
This is the transfer-function form of the compensator. | Out[63]= |  |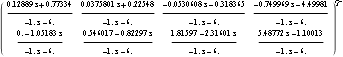
This closes the feedback loops with this compensator, using negative output feedback. This confirms that the desired closed-loop poles have again been attained. | Out[66]= |  |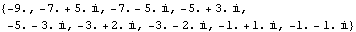
The gains required for this latter compensator with open-loop pole at s = -6 are less than those required for the compensator determined with open-loop pole at s = -8. For systems where the specified compensator poles are achievable, you may wish to explore the results obtained with different compensator poles. |
