NDEigensystem::fembdcc NDEigenvalues::fembdcc NDSolve::fembdcc NDSolveValue::fembdcc ParametricNDSolve::fembdcc ParametricNDSolveValue::fembdcc InitializePDECoefficients::femcnmd
例題
例 (2)
以下の偏微分方程式は,与えられた拡散係数に対してメッセージを発する:
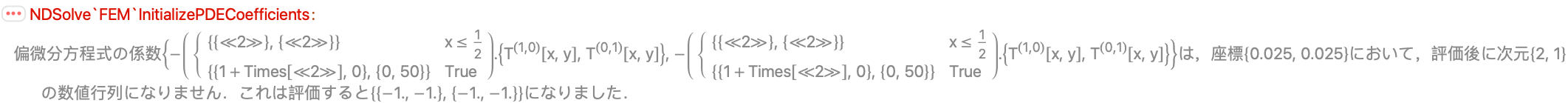
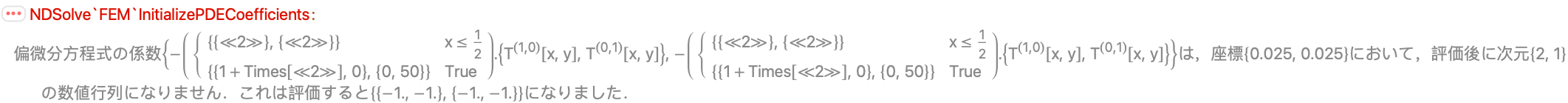
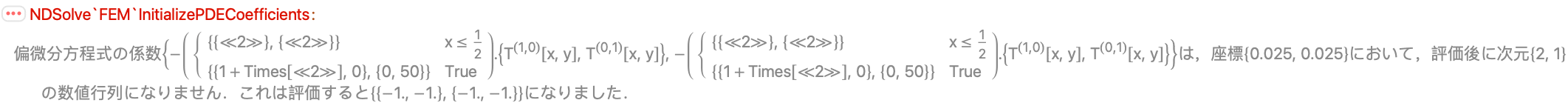
これは,自動的な線形化の際に,係数の導関数が形成できないことから起る.解決策として,係数をPiecewiseを返す行列としてではなく,Piecewiseのスカラー係数を含む行列として書くことができる:
偏微分方程式係数として使われる,以下のコンパイル関数を考える:
最初の警告メッセージは,コンパイル関数が機械サイズの実数以外のもので評価されたことを示す.実際,このメッセージは,記号の引数でコンパイル関数を評価したことから発するものである:
このメッセージについては,ここにより詳しく説明されている.コンパイル関数は,コンパイルされたコードの本体を記号式として返し,その後NDSolveが偏微分方程式を解く.NDSolveが返す警告メッセージは,これが対流支配の偏微分方程式であることを示し,そのことについてはここに説明がある.メッセージを発しながらも,NDSolveが偏微分方程式の解を返すということに注意されたい.
記号入力について評価しないコンパイル関数を指定して,このような問題に対処せずに済むようにしたい場合もあるかもしれない:
cfをNDSolveで偏微分方程式の係数として使うと問題が起る.なぜ問題が起るのか,どのようにしてこれを避けることができるのかを理解するためには,少し脇道に逸れる必要がある.
偏微分方程式の設定は有限要素法をトリガする.何が有限要素法をトリガするのかについては,ここに説明がある.有限要素法は,ここに説明されているように,非常に特別の形式の偏微分方程式のみを扱うことができる:
この偏微分方程式を解くために起ることは,係数 ![]() が発散に引き込まれ,
が発散に引き込まれ,![]() 項を調整することで以下のように補われるのである:
項を調整することで以下のように補われるのである:
記号的に評価されないコンパイル関数は,この偏微分方程式の再構築の過程で問題を起す:

このためNDSolveがエラーを発する.これに対処する方法は2つある.1つ目は,可能であれば,記号係数を与える方法である.そうすると,NDSolveは解を求めることができる:
もう一つは,手動で導関数を構築して,係数を指定する方法である: