Finite Element Method Usage Tips
Introduction
The aim of this tutorial is to point out possible issues when using the finite element method with NDSolve and related functions such as NDEigensystem and offer best practices to avoid potential issues.
Monitoring the Solution Progress of Nonlinear Stationary Partial Differential Equations
The solution of partial differential equations can be time consuming. This is particularly true for large-scale nonlinear PDEs. To monitor the solution process of nonlinear PDEs, EvaluationMonitor and StepMonitor can be used. In the following example, a nonlinear PDE is solved and the number of function evaluations, steps and Jacobian evaluations is monitored. In this specific example, a Pause command has been added to slow the solution process down for better inspection. In a scenario where the PDE solution process is slow per se, the use of Pause is, of course, not needed.
Monitoring Progress of Time Integration of Transient Partial Differential Equations
Time integration of partial differential equations can take time. This is especially true if the boundary conditions or coefficients are time dependent or if the PDE region at hand is three dimensional. An easy way to monitor progress of an integration of a transient PDE is by using an EvaluationMonitor.
Using the EvaluationMonitor within NDSolve works as in other cases. Here is an example wave equation with a time-dependent Dirichlet condition.
Step Size Plots for Transient Partial Differential Equations
Transient PDE models deal with simulations that vary over time. When solving transient partial differential equations (PDEs), NDSolve and related functions begin with the given initial conditions and then start to construct the solution of the PDE beyond that. NDSolve computes the evolution of the dependent variables using an adaptive time integration method. Adaptive means that the size of the time steps taken can vary according to how much dynamics is present at a given point in time.
In some other finite element software programs, it is the responsibility of the user to check that the time integration went smoothly. This is never needed when using NDSolve. NDSolve will automatically issue a message if the time integration, for whatever reason, could not be performed according to the, possibly implicitly requested, accuracy or precision goal, or when the step size became too small to proceed. Never the less, it can be instructional to look at the step sizes NDSolve took to gain an understanding of what the dynamics of the PDE is like at certain points in time.
To visualize how the step size evolves during the simulation process, one can use StepDataPlot, which returns the step sizes used in the NDSolve solution on a logarithmic scale. In order to use StepDataPlot, one needs to load the Numerical Differential Equation Solving package.
The visualization of the step size plot is best illustrated by an example.
In this example, a time-dependent heat transfer equation is set up using the default parameters of HeatTransferPDEComponent: 
, 
and 
, with a heat source 
given by 
.
The equation is solved with thermally insulated boundary conditions over all boundaries, which is the default setup when no boundary conditions are given.
A step size plot with increasing step size values on the 
axis shows that the time-dependent solver takes larger time steps. Some other FEM software displays its step size plots by plotting the reciprocal of the step size.
Solving Memory-Intensive PDEs
Some of the examples presented here require a large amount of RAM memory.
The amount of memory needed by NDSolve to solve a particular problem with the finite element method is proportional to the number of equations and the space dimension in which you are operating. For coupled systems in 3D, the amount of memory provided by the underlying hardware can be a barrier. The following section identifies easy-to-use options to alleviate this potential barrier.
The first thing to do is to set the $HistoryLength to 0. This avoids storing previous results stored in Out.
During the finite element analysis there are two key memory bottlenecks. The first is the creation of the discretization and the second is the solution (LinearSolve) of the system of equations. NDSolve provides options to both mesh generation and the LinearSolve step that have an effect on the memory requirement during discretization and solving. As a rough estimate, the number of coordinates in the internal generated mesh multiplied by the spatial dimension gives the degrees of freedom (number of rows and columns) of the discretized system matrix to be generated.
As an example, consider a stress operator from linear elasticity, explained in detail in the solid mechanics monograph. The stress operator is a system of three coupled PDEs in 3D space. Since the main focus of this section is to create a large system of equations, no additional information about the PDE itself is presented.
A series of measurements illustrates how various options influence the solution time and the amount of memory needed to find a solution. For this purpose, a helper function is implemented. The function receives as input any number of NDSolve options and returns the time and the amount of memory in MB needed to solve the PDE. It is also instructive to get a feeling for the size of the system matrices NDSolve internally establishes. The size of the system matrices is its degrees of freedom, or in other words, the number of rows and columns in the system matrices.
The default settings in NDSolve are set up such that the solution is accurate and found fairly efficiently. To make this example applicable for a larger class of computers, tetrahedron elements are used. The use of these results in smaller system matrices.
With the default setting, NDSolve with a finite element discretization will call LinearSolve with "Pardiso" as the solver method. This will route to a direct solver that is very accurate but has a high requirement of available memory.
Typically, solvers other than the default "Pardiso" solver are not as efficient.
An option of the "Pardiso" solver to reduce the amount of memory required to solve a particular problem is its out-of-core functionality. This means that, among other things, the LU factors are stored on disk and do not occupy RAM memory. This allows somewhat larger problems to be solved. One thing to keep in mind is that even though some aspects of the solution process are stored on disk, the system matrix will still need to fit completely into the computer's RAM.
Note that due to the finer mesh used, the number of degrees of freedom has been increased considerably. One thing to keep in mind is that when there is enough RAM memory available, then the out-of-core functionality will be slower. This option should be only be used if NDSolve runs out of memory and not on a hunch.
Another way to reduce the memory consumption is to have NDSolve generate a mesh with fewer elements.
This has reduced both solution time and memory requirements at the price of accuracy. How many elements a mesh needs to represent an accurate solution is problem dependent. A good method is to start with a coarse mesh and refine until the solutions stop differing substantially.
A way to further reduce the amount of memory needed for computing the solution is to use a mesh that is only first-order accurate.
This has reduced both solution time and memory requirements at the price of accuracy. Making use of a first-order mesh results in much smaller system matrices, which can be solved more efficiently. Using a first-order mesh may significantly reduce accuracy.
Another approach that can be used to solve a large-scale problem is to solve it in two steps, first on a coarse, possibly first-order mesh. The solution found there is then used as a starting vector for an iterative solver.
The options discussed here can also be combined. A more in-depth treatise of options that can be given to NDSolve can be found in the finite element tutorial Finite Element Options.
Memory Consumption During Repeated Evaluation
When a partial differential equation is solved multiple times repetitively, an increasing amount of memory may be consumed in consecutive evaluations. To illustrate this, a parametric function is created and then evaluated repetitively.
Next, the parametric function is evaluated several times and the memory usage is reported after every 10th evaluation.
The increased memory consumption is a result of caching data. The caching of data is done to increase the speed of the evaluation. In situations where memory constraints are tight, an occasional clearing of the cache will remove the stored data. The clearing of the cache can be done with ClearSystemCache.
Caching during derivative computation also contributes to memory consumption.
Extrapolation of Solution Domains
This section has been moved to the NDSolve Options for Finite Elements.
Overshoot/Undershoot of Discontinuous Coefficients
In previous versions, Wolfram Language had only limited capability to deal with interpolation of discontinuous coefficients in a region directly. This shortcoming has been remediated in Version 14.0. Consider an example.
When two distinct values are assigned for each region, for example, white 0 and gray 1, a discontinuity occurs at the regions' interface.
Note that EvaluateOnElementMesh returns a DiscontinuousInterpolatingFunction. It does so if the mesh given has more than one material marker. For more information on material markers, please refer to the section Markers in the Element Mesh Generation tutorial.
Note that the discontinuous interpolating function has sharp features at the interface. Also, the minimum and maximum values are in the range of the function given.
One can switch back to the old behavior, if desired for some reason. "EvaluateOnElementMesh" will return an InterpolatingFunction if the option "DiscontinuousInterpolation" False is specified.
Note that the extreme values of the interpolating function exceed the designated range 
.
We can control exactly how DiscontinuousInterpolatingFunction behaves at the interface.
It can be desirable to choose the value at the interface. This can be done by setting the "MarkerPriority". The way the DiscontinuousInterpolatingFunction works is that it looks at the mesh element markers of the mesh and prioritizes the evaluation at the discontinuous interface according to the markers of the mesh.
This means that if there is a point at the interface, then the value assigned to marker 0 will be prioritized over the value assigned to marker 1.
Next, regenerate the DiscontinuousInterpolatingFunction, this time, however, of a different marker priority.
Note that the plot in general is the same, with the exception that now at the interface the default value associated with marker 1 takes precedence over values at marker 0.
Stabilization of Convection-Dominated Equations
Consider a convection-diffusion type of equation.
Details about the coefficients can be found in InitializePDECoefficients.
In a situation where the convective component 
becomes large, the solution of the PDE may become unstable, as shown in the following example.
The message indicates that the solution may not be stable. The Péclet number is a dimensionless number and expresses the ratio between convection and diffusion of a physical quantity. The Péclet number is computed as
where 
is the convective component, 
is a minimum element diameter, and 
is the diffusion coefficient. If the Péclet number is larger than the mesh order, then the stability of the solution may become a concern and the message is given.
The result is disastrous. There are a few things that can be done in such situations. First, however, investigate how the Péclet number is computed.
In the case that the convection term 
or the diffusion term 
is a function of the spatial coordinates, the term is evaluated at a single test coordinate. This test coordinate can be changed by specifying the "VerificationData" option discussed in InitializePDECoefficients.
Note that the instability also has to do with the boundary conditions specified.
The boundary conditions at 
and 
specify a value for the dependent variable 
that inhibits the flow of 
in that direction. They are blocking the "outflow".
Not enforcing Dirichlet conditions on 
and 
will also avoid the instability.
Now, the boundary conditions may not always be chosen. One way to improve the stability of the solution is to add so-called artificial diffusion. This artificial diffusion is then added to the diffusive term in order to stabilize the PDE.
Note that the newly computed Péclet number is smaller than the mesh order.
This is already much better. The additional diffusion smears out the solution to some extent. To further improve this, the artificial diffusion can be made to follow the streamline of 
. This, however, will only work if the flow field 
is divergence free. This method is called streamline upwind Petrov–Galerkin (SUPG).
The SUPG solution is less diffusive for 
compared to the solution computed with pure artificial diffusion.
The disadvantage with these methods is that the PDE is modified. This may not always be a good approach. As an alternative, the mesh can be modified. For more information about mesh generation, please consult "Element Mesh Generation".
The solution is improved compared to the previous examples, at the cost of some additional computational time. In principal, it would be sufficient to only refine the right and top boundaries of the mesh. This would then decrease the computational time.
As a next step, we can make use of ToGradedMesh to build a fine mesh that is graded toward the right and top.
Stabilization of Convection-Dominated Time-Dependent Equations
The following section shows how numerical instabilities can come up in convection dominant time dependent equations. This section shows the use of artificial diffusion to minimize numerical instabilities caused by a lack of diffusivity in an equation.
As an example, consider a coupled first-order sound wave equation.
The equation has two dependent variables, 
and 
. Since there is no diffusion term in the system, the solution of the PDE may become unstable.
To solve the system, specify the coefficients 
and 
, and then set up the wave equation PDE operator.
As boundary conditions, sinusoidal sound sources of angular frequency 
are placed at the left boundary.
Since this is a time-dependent PDE, initial conditions must be specified.
To solve the wave equation, the wavelength 
of a sound wave needs to be resolved by a sufficiently fine mesh 
in order to get an accurate numerical solution. Set the grid size 
to be at least sixty times smaller than the sound wavelength.
The ripples in the solution come from a numerical instability. To improve the stability, artificial diffusion can be added to the PDE system.
Note that the Péclet number can be used to estimate the required artificial diffusion only if the PDE contains a single dependent variable. Since there is now a system of equations with two unknown variables, a diffusion coefficient 
must be manually picked.
is a manually chosen parameter that controls the effect of artificial diffusion. Since the PDE is modified when adding artificial diffusion, users should carefully pick the value of ϵ between 1 and 10 that stabilizes the solution without reducing the fidelity.
Note that the stability has improved with artificial diffusion. Next, the numerical results are compared to the analytical result.
Since the PDE is modified, adding artificial diffusion will smooth out the gradient change of the solution. That is why it produces a larger error at the front of the wave.
The Coefficient Form of a PDE
In this example, the importance of the coefficient form of PDEs for the finite element method is demonstrated. The coefficient form for a single dependent variable PDE is given in equation (1).
Details about the coefficients can be found in InitializePDECoefficients.
The PDE is defined in 
. Here 
is the dependent variable for which a solution is sought. The coefficients 
, 
, 
, and 
are scalars; 
, 
, and 
are vectors; and 
is an 
×
matrix.
The key point of this example is that this equation (and coupled versions of it) is in essence the only equation the finite element method can solve. To emphasize this point, consider the simpler equation (2).
Set up the equation and its coefficients. As a spatial domain for the PDE, 
is used, and the time integration will be set up to stop at 
. The diffusion coefficient 
is set to 1, which will internally get transformed to the identity matrix. For the damping coefficient 
, a piecewise continuous function is used that has the value of 1 for values of 
, and 2 otherwise.
One could be tempted to reformulate equation (4) in the following manner.
Clearly, solution 1 and solution 2 differ. To investigate what happens, write a little helper function that extracts the actually parsed PDE coefficients from NDSolve data structures. For more information on the internal workings of the finite element method, please consult the Finite Element Programming tutorial.
The coefficients for equation (7) look as expected. An alternative to the coefficient extraction is to look at how the differential equation was parsed.
There is nothing unusual so far.
The coefficients for equation (9) come as a surprise. The coefficient 
got pulled into the diffusion coefficient 
. Why is that? The key is to understand that the finite element method can only solve this type of equation.
Note that there is no coefficient in front of the term 
. To get equations of the type 
to work, 
is reset to 
and 
is adjusted to get rid of the derivative caused by 
. Here is an example.
Following the same procedure for the equation (10), you get:
This is effectively the same as explicitly specifying 
. Mathematically, because of the discontinuity, the coefficient 
is like a Dirac delta function, which would be omitted in the time integration anyway.
For time-dependent PDEs with a discontinuous diffusion coefficient, it is best to arrange the equations such that the coefficient is eliminated from the diffusion term.
Formal Partial Differential Equations
Formal partial differential equations are equations that have Inactive components. When Inactive PDEs are typeset, then the Inactive PDE components are shown in gray. This section explains when PDEs need to be inactive.
The main point of using Inactive PDEs is to prevent premature evaluation of the PDE coefficients. For example, the evaluated divergence of a gradient has an effect on what a NeumannValue means.
With the inactive version, one has exact control over what a possible NeumannValue means in relation to the equation, which is not the case in the active form. NDSolve and related functions cannot perform this operation automatically because NDSolve does not hold it's arguments unevaluated. In other words, NDSolve does not have an Attributes, HoldFirst or HoldAll.
Another example where an Inactive form of the equation is needed is when the PDE coefficients are unsymmetric. An example is a plane stress operator. For Young's modulus and Poisson's ratio, values for steel are used.
The first eigenvalue and eigenfunction of a beam held fixed at the left with length 10 meters and height 0.7 meters are computed.
As a means of comparison, the first resonance frequency utilizing Euler–Bernoulli beam theory is computed analytically.
Compare the difference in results; about half the difference is attributable to the different theoretical approaches.
Next, the Active version of the PDE is inspected and the resulting resonance frequency is computed.
The above result is wrong. What happened? In short, the non-inactive version cannot account for unsymmetric coefficients. Looking at the original inactive PDE of the four coefficient matrices, two, the off-diagonal ones, are not symmetric.
In other words, even before NDEigensystem (and other related functions like NDSolve) can parse the PDE in its intended form, it will have evaluated.
From the evaluated PDE, there is no way to recover the antisymmetric coefficients. For this reason Inactive has been introduced. For antisymmetric coefficients, the Inactive version of the PDE is a must.
To inspect the coefficients that have been parsed, NDSolve`ProcessEquations can be used on the time-dependent equation input of NDEigensystem. If the input to NDEigensystem is in operator form, it will have to be converted to a time-dependent equation for NDSolve`ProcessEquations to work on the input. Note that arbitrary initial conditions 
and an arbitrary time integration interval 
need to be specified.
A second example where an inactive form of the equation is needed is nonlinear PDEs that have a derivative of the dependent variable in the diffusion coefficient, like the following PDE.
The diffusion coefficient 
is nonlinear because it contains the dependent variable 
.
If the equation at hand is not in inactive form, NDSolve will not be able to solve the PDE.
Currently NDSolve cannot solve stationary PDEs that have a higher than first-order derivative involving the dependent variable in any of the coefficients. This is explained as follows: The activated operator needs to match the coefficient form 
. As a first step, the diffusion coefficient is set as 
.
Inserting the diffusion coefficient 
in the coefficient form results in the following.
The remaining term 
is compensated by also setting 
in the coefficient form.
However, evaluating 
returns a higher than first-order derivative in the 
coefficient, which the finite element method in NDSolve currently cannot solve.
The purpose of Inactive for the finite element method is to set up the coefficient form of a PDE given in equation (11) as a formal partial differential equation. All mathematical operators of equation (12) can be inactive. In other words, an Inactive PDE can contain Inactive[Div] and Inactive[Grad] components but not inactive D such as Inactive[D] or inactive Derivative such as Inactive[Derivative] components, as this functionality can be expressed with Div and Grad.
From time to time it is useful to inspect how a PDE has been parsed by NDSolve. This can be done with GetInactivePDE.
For more information, see the section The Coefficient Form of a PDE.
NeumannValue and Formal Partial Differential Equations
This section explains the interaction between formal partial differential equations and NeumannValue. In the stationary case, a partial differential equation can be expressed as follows:
Details about the coefficients can be found in InitializePDECoefficients.
On the other hand, generalized Neumann boundary values specify a value 
. The value 
prescribes a flux over the outward normal on some part of the boundary:
The derivation of the Neumann boundary value is outlined in Partial Differential Equations and Boundary Conditions. It is important to note that the coefficients 
, 
, and 
in equation (13) are not specified directly by the use of NeumannValue. The coefficients 
, 
, and 
are specified in equation (14). The use of NeumannValue will replace 
with the value of 
on the boundary.
Now, the usage of Div and Grad alone is not enough to fully specify equation (15). Consider the specification of
and its corresponding Neumann value:
Consider a case where 
is given as 
, 
is the identity matrix and 
is a zero vector. Note that the evaluation of the divergence results in
where 
is 
and 
is the divergence of 
, 
in this example. Equations (16) and (17) are equivalent.
The evaluation poses a problem, however. Even though the equations are equivalent, the Neumann specifications are not. The corresponding Neumann value for equation (18) has implicitly changed to
To illustrate this further, a helper function is created that parses a PDE and extracts the PDE coefficient data from the finite element data, as explained in "Finite Element Programming".
PDECoefficientData is a data structure that contains the parsed PDE coefficients.
During evaluation, the coefficient 
split into a 
and 
term. The proper mechanism to input differential equations where coefficients are evaluated prematurely is by either Inactivate or directly through the use of Inactive.
If a γ term is present one might use the following inactive PDE:
The following example illustrates the difference in meaning of an active and inactive PDE with respect to Neumann values, from a practical perspective. The example shows a diffusion confined in a region 
subject to a biasing potential 
.
Dirichlet boundary conditions are set up at the top and bottom (
) of the region with a potential of 1 and 0, respectively.
At the remaining two sides (
) natural boundary conditions (Neumann zero) apply. This means zero flux across these two edges.
The PDE to be modeled is given by:
and its corresponding Neumann value at 
is
First the satisfaction of the Neumann values at 
is inspected.
of the inactive operator over the edges with the Neumann zero value implicitly specified. The normal derivative is in the direction of 
.With zero flux boundary conditions at 
(no flux across these two edges) and no source terms, the flux into the box at 
should be the same as the flux out of the box at 
.
of the inactive operator over the edges with the Dirichlet condition. The normal derivative is in the direction of 
.The flux into the box is roughly the same as the flux out of the box. As a comparison, the activated PDE is solved.
The 
coefficient is parsed as a convection and a reaction coefficient.
In the activated case, the boundary condition computed is 
.
of the activated operator over the edges with the Dirichlet condition. The normal derivative is in the direction of 
.From time to time, it is useful to inspect how a PDE has been parsed by NDSolve. This can be done with GetInactivePDE.
For more information, see the section The Coefficient Form of a PDE.
Efficient Evaluation of PDE Coefficients
The coefficients in a PDE need not be constants. In this example, the diffusion coefficient 
depends on the position in a simulation region.
It is important to understand the evaluation order of the coefficients specified because it can have an effect on the performance of the simulation. First, a mesh with an internal boundary is generated.
Once the mesh is set up, the PDE with an unspecified diffusion coefficient 
is set up.
The diffusion coefficient 
is set up in such a way that in the inner region the value of the diffusion coefficient 
, while outside of that region the diffusion coefficient 
.
The simulation worked as expected. Look more closely at the diffusion coefficient 
and note that the branches of the If statement are not evaluated.
The reason that the If statement does not evaluate its branch arguments is that the If statement has attributes set that prevent the evaluation.
The fact that the If statement in diffusion coefficient 
does not have its branch arguments evaluated means that in every call the variables have to be looked up. As a consequence, the If statement cannot be compiled and will use the standard evaluator, which will be slower in this case.
When creating a coefficient function that has all its arguments evaluated, With can be useful.
Note that now the If statement has all arguments evaluated.
For small examples like this one, this may not be much of an issue—but as soon as the simulation becomes larger, fully evaluated coefficients are something to think about.
A second, easier-to-use alternative to using With for injecting content into the If statement is to use Piecewise. Piecewise does not have any attributes associated with it and thus evaluates its arguments.
Note that the Piecewise statement has all arguments evaluated.
From a speed perspective, the Piecewise construct should be as efficient as the With/If construct.
Note that when PDE components like the HeatTransferPDEComponent are used to set up the PDE, an efficient coefficient substitution happens automatically.
Note how the symbolic parameter values have been replaced by the actual numeric values.
Another scenario where essentially the same issue comes up is when coefficients are hidden behind a SetDelayed.
In the second case, the test is evaluated symbolically and is more efficient when used as a coefficient in a PDE model.
Efficient Evaluation of Interpolating Functions in PDE Coefficients
PDE coefficients can be interpolating functions. A very efficient evaluation of the interpolating functions can be done if the interpolating function can make use of the same mesh as the PDE is solved over.
Note that when the mesh in the interpolating function is the same as the mesh used for the PDE, solving the execution time is smaller.
The most efficient way is to give an expression directly, if possible.
The Relation between NeumannValue and Boundary Derivatives
The following example explains the relation of a NeumannValue and boundary derivatives, and is set up such that the parameters are easy to modify. First, the region 
is specified.
The PDE has one dependent variable 
. Note that since this is a one-dimensional system, the diffusion coefficient 
is a 1×1 matrix, which can be specified as a number.
Dirichlet boundary conditions specify a value 
for the dependent variable 
.
Neumann values are specified by the following form.
Next, the boundary conditions are set up.
Note how in the DSolveValue formulation of the equation, the generalized Neumann boundary equation has to be given explicitly, and how the coefficients match those in the PDE.
To compare the analytical result to the numerical result, make a plot of the difference between the two.
Ordering of Dependent Variable Names
In some cases, when analyzing coupled systems of PDEs, the finite element method as implemented in NDSolve may return what seem to be unexpected results. This section explains when this happens and presents solutions to avoid the problem. In the last section, a more in-depth explanation is presented.
First a system of equations with appropriate boundary conditions and a region are set up.
The dependent variables for this example are u, v and w. The system is solved and a visualization of the dependent variable w is given.
In a second experiment, the dependent variable name w is changed to p and the system of equations is solved yet again.
The result is unexpected. Before explaining in detail what happens, two ways to enforce the expected behavior are presented.
One option is to specify the dependent variables through the "DependentVariable" method option of NDSolve.
Specifying the "DependentVariable" method option will enforce the order in which the dependent variables are discretized to the order given. This is explained in further detail in the following.
For this specific case, NDSolve offers a finite element method option to specify an interpolation order that should be used for the dependent variables during the discretization of the PDE. The specification of the interpolation order will implicitly also enforce the same ordering of the equations and the dependent variables.
Generally, specifying the same interpolation order for each dependent variable is fine. The reduction of the interpolation order is not central to the issue at hand. In this specific case, the equations are fluid flow equations (Stoke's flow), and stabilization can be enforced if the pressure variable's Interpolation order is one less than the interpolation order for the velocities u and v.
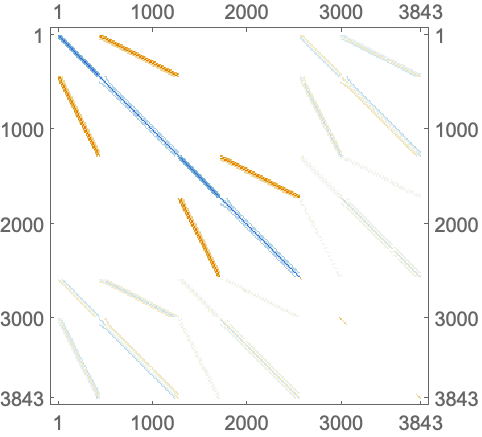
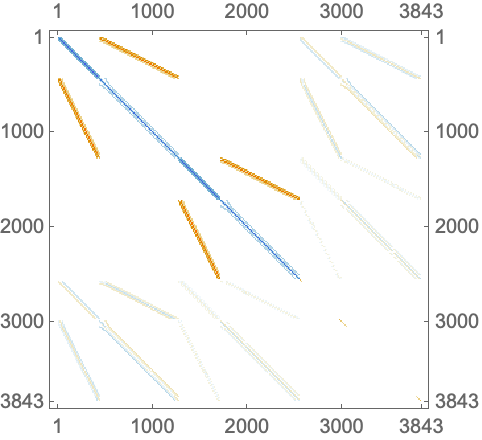
To get an intuition of what the underlying problem is, the assembled discretized system matrix for both cases is displayed.
To investigate this behavior further, an NDSolve state object is created.
Note that the ordering of the dependent variables in the FEMMethodData in the FiniteElementData is {p,u,v}.
Inspecting the diffusion and convection coefficients of the PDECoefficientData reveals the structure of the coupled PDE coefficients.
When the finite element interpolation order method option is set, the coefficient structure is adjusted to the canonical order of the dependent variables.
In fact, reordering the equations' input to match the canonical order of the dependent variables also gives the expected result.
A remaining question is, why can this reordering not happen automatically?
The inherent challenge is that the boundary conditions specified can only be applied to diagonal components of the coefficients. The reason is that the way the boundary conditions are entered causes the information about how a specific boundary condition relates to a specific equation in the PDE to be lost.
Here each sublist has two parts. The first part indicates the row and column in which the second part—the boundary condition—will be applied during the discretization.
Another option is to associate the Dirichlet boundary conditions with the respective equation to which they are related.
In summary, the best option is to specify the interpolation order.
Verifying Solutions
A way to verify a solution of a differential equation as obtained from NDSolve and related functions is to reinsert the solution in the differential equation at hand.
From the preceding, one might think that reinserting the solution into the differential equation is an acceptable way to verify the solution of a differential equation. This is not always the case.
The result suggests that the solution is much less accurate than the previous example. Is that really the case?
In the preceding example, an implicit assumption was made: when the solution is reinserted into the differential equation, higher-order derivatives of the InterpolatingFunction have to be computed. However, this derivative recovery process is not without error and does not compare well to the scale of 
. A mesh order larger than two would improve the situation and a mesh order of 1 would worsen it further. Try it out.
Ideally, a solution to differential equations is checked without introducing further numerical errors while verifying the solution. To do so, the method of manufactured solutions is useful. If an analytical solution to the differential equation were present, then the computed solution could be verified against this analytical solution. The idea of manufactured solutions is choose an arbitrary solution and then to modify the original differential equation such that the chosen solution is an actual solution.
Inserting the chosen analytical solution into the original differential equation results in a new right-hand-side term, 
. When the original equation is set equal to this new right-hand side 
, then the chosen solution Sin is by construction a solution to the new differential equation.
The error for this chosen analytical solution case is much less than what reinserting the solution form NDSolveValue into the original equation suggested it would be. The advantage of this approach is that no new numerical errors are introduced when the solution is verified.