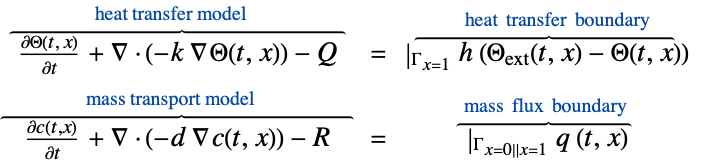HeatTransferPDEComponent[vars,pars]
yields a heat transfer PDE term with variables vars and parameters pars.


HeatTransferPDEComponent
HeatTransferPDEComponent[vars,pars]
yields a heat transfer PDE term with variables vars and parameters pars.
Details




- HeatTransferPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- HeatTransferPDEComponent models the generation and propagation of thermal energy in physical systems by mechanisms such as convection, conduction and radiation.
- HeatTransferPDEComponent models heat transfer phenomena with dependent variable temperature
 in [
in [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTransferPDEComponent.en/4.png) ], independent variables
], independent variables 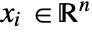 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/HeatTransferPDEComponent.en/6.png) ] and time variable
] and time variable  in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/HeatTransferPDEComponent.en/8.png) ].
]. - Stationary variables vars are vars={Θ[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={Θ[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative time-dependent heat transfer model HeatTransferPDEComponent is based on a convection-diffusion model with mass density
 , specific heat capacity
, specific heat capacity  , thermal conductivity
, thermal conductivity 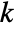 , convection velocity vector
, convection velocity vector  and heat source
and heat source  :
: - The non-conservative stationary heat transfer PDE term is given by:
- The implicit default boundary condition for the non-conservative model is a HeatOutflowValue.
- The difference between the non-conservative model and the conservative model is the treatment of a convection velocity
 .
. - The units of the heat transfer model terms are in [
![TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/17.png) ], or equivalently in [
], or equivalently in [![TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , {"m", ^, 3}, , "s", , ")"}, joules per meter cubed second, {{(, "Joules", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , {"m", ^, 3}, , "s", , ")"}, joules per meter cubed second, {{(, "Joules", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/18.png) ].
]. - The following parameters pars can be given:
-
parameter default symbol "HeatConvectionVelocity" {0,…}  , flow velocity [
, flow velocity [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/20.png) ]
]"HeatSource" 0  , heat source [
, heat source [![TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/22.png) ]
]"MassDensity" 1  , density [
, density [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/24.png) ]
]
"Material" Automatic 
"ModelForm" "NonConservative" none "RegionSymmetry" None 
"SpecificHeatCapacity" 1  , specific heat capacity [
, specific heat capacity [![TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , "kg", , "K", , ")"}, joules per kilogram kelvin, {{(, "Joules", )}, /, {(, {"Kilograms", , "Kelvins"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , "kg", , "K", , ")"}, joules per kilogram kelvin, {{(, "Joules", )}, /, {(, {"Kilograms", , "Kelvins"}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/28.png) ]
]"ThermalConductivity" IdentityMatrix  , thermal conductivity [
, thermal conductivity [![TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , "m", , "K", , ")"}, watts per meter kelvin, {{(, "Watts", )}, /, {(, {"Meters", , "Kelvins"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , "m", , "K", , ")"}, watts per meter kelvin, {{(, "Watts", )}, /, {(, {"Meters", , "Kelvins"}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.en/30.png)
- All parameters may depend on any of
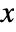 ,
,  and
and  , as well as other dependent variables.
, as well as other dependent variables. - The number of independent variables
 determines the dimensions of
determines the dimensions of  and the length of
and the length of 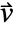 .
. - Sometimes the heat equation is specified with a thermal diffusivity. The thermal diffusivity is the thermal conductivity divided by the density and the specific heat capacity at constant pressure.
- The thermal convection velocity specifies the velocity
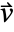 with which a fluid transports heat. If no fluid is present, the thermal convection velocity is 0.
with which a fluid transports heat. If no fluid is present, the thermal convection velocity is 0. - A heat source
 models thermal energy that is introduced (positive) or removed (negative) from the system.
models thermal energy that is introduced (positive) or removed (negative) from the system. - A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
- "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
-
dimension reduction equation 1D 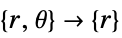

2D 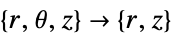
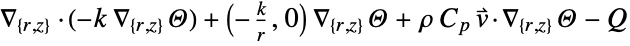
- The input specification for the parameters is exactly the same as for their corresponding operator terms.
- Coupled equations can be generated with the same input specification as with the corresponding operator terms.
- If no parameters are specified, the default heat transfer PDE is:
- If the HeatTransferPDEComponent depends on parameters
 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters  are replaced with
are replaced with  .
.

Examples
open all close allBasic Examples (4)
Scope (7)
Basic Examples (2)
1D (1)
2D (1)
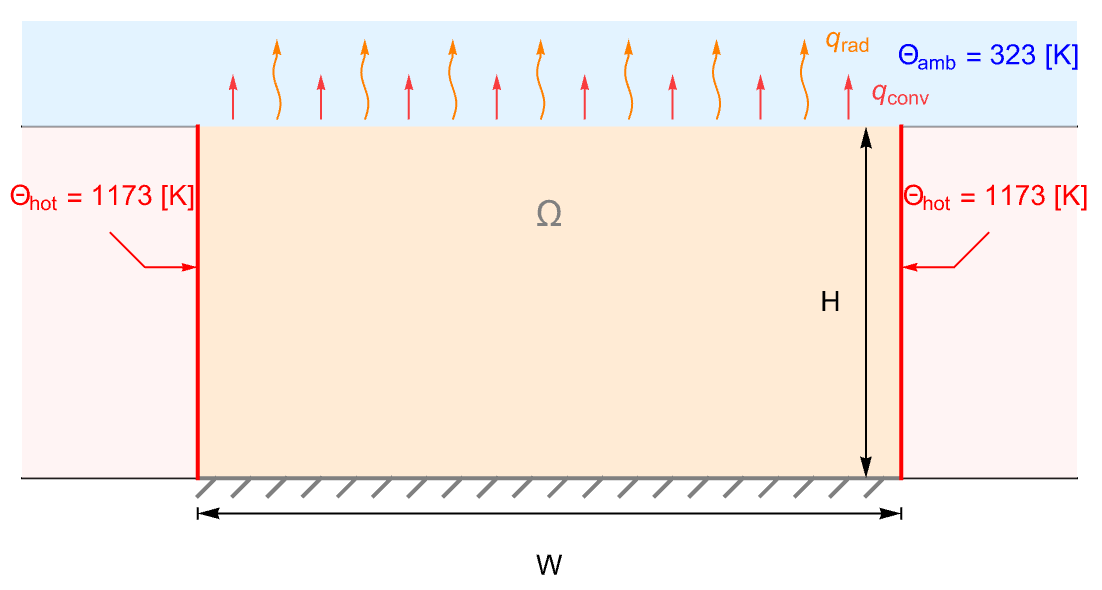
Model a ceramic strip that is embedded in a high-thermal-conductive material. The side boundaries of the strip are maintained at a constant temperature ![]() . The top surface of the strip is losing heat via both heat convection and heat radiation to the ambient environment at
. The top surface of the strip is losing heat via both heat convection and heat radiation to the ambient environment at ![]() . The bottom boundary is assumed to be thermally insulated:
. The bottom boundary is assumed to be thermally insulated:
Model a temperature field and the thermal radiation and thermal transfer with:
Set up the heat transfer model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify thermal conductivity ![]() :
:
Set up temperature surface boundary conditions ![]() at the left and right boundaries:
at the left and right boundaries:
Set up a heat transfer boundary condition on the top surface:
Also set up a thermal radiation boundary condition on the top surface:
3D (1)
Model a temperature field with two heat conditions at the sides and an orthotropic thermal conductivity ![]() :
:
Set up the heat transfer model variables ![]() :
:
Specify an orthotropic thermal conductivity ![]() :
:
Specify heat surface conditions:
Set up the equation with a thermal heat flux ![]() of
of ![]() applied at the left end for the first 300 seconds:
applied at the left end for the first 300 seconds:
Time Dependent (1)
Model a temperature field and a thermal heat flux through part of the boundary with:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters mass density ![]() , specific heat capacity
, specific heat capacity ![]() and thermal conductivity
and thermal conductivity ![]() :
:
Specify a thermal heat flux ![]() of
of ![]() applied at the left end for the first 300 seconds:
applied at the left end for the first 300 seconds:
Set up the equation with a thermal heat flux ![]() of
of ![]() applied at the left end for the first 300 seconds:
applied at the left end for the first 300 seconds:
Time-Dependent Nonlinear (1)
Model a temperature field with a nonlinear heat conductivity term with:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters mass density ![]() , specific heat capacity
, specific heat capacity ![]() and a nonlinear thermal conductivity
and a nonlinear thermal conductivity ![]() :
:
Specify a thermal heat flux ![]() of
of ![]() applied at the left end for the first 300 seconds:
applied at the left end for the first 300 seconds:
Set up the equation with a thermal heat flux ![]() of
of ![]() applied at the left end for the first 300 seconds:
applied at the left end for the first 300 seconds:
Applications (7)
Boundary Conditions (5)
Compute the temperature field with model variables ![]() and parameters
and parameters ![]() with a thermal surface
with a thermal surface ![]() of
of ![]() at the left boundary:
at the left boundary:
Visualize the solution and note the sinusoidal temperature change on the left:
Compute the temperature field with model variables ![]() parameters
parameters ![]() :
:
Set up the equation with a thermal outflow boundary at the right end:
Define the initial temperature field:
Visualize the solution and note how the energy leaves the domain through the thermal outflow boundary on the right:
Model a temperature field and a thermal radiation boundary with:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters mass density ![]() , specific heat capacity
, specific heat capacity ![]() and thermal conductivity
and thermal conductivity ![]() :
:
Specify boundary condition parameters with a constant ambient temperature ![]() of
of ![]()
![]() and a surface emissivity
and a surface emissivity ![]() of
of ![]() :
:
Model a temperature field with heat transfer boundary:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters mass density ![]() , specific heat capacity
, specific heat capacity ![]() and thermal conductivity
and thermal conductivity ![]() :
:
Specify boundary condition parameters with an external flow temperature ![]() of
of ![]()
![]() and a heat transfer coefficient
and a heat transfer coefficient ![]() of
of ![]() :
:
Model a temperature field and a thermal insulation and a thermal heat flux boundary with:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters mass density ![]() , specific heat capacity
, specific heat capacity ![]() and thermal conductivity
and thermal conductivity ![]() :
:
Coupled Equations (2)
Solve a coupled heat and mass transport model:
Set up the heat transfer mass transport model variables ![]() :
:
Specify heat transfer and mass transport model parameters, heat source ![]() , thermal conductivity
, thermal conductivity ![]() , mass diffusivity
, mass diffusivity ![]() and mass source
and mass source ![]() :
:
Set up the model and initial conditions:
Solve a coupled heat transfer and mass transport model with a thermal transfer value and a mass flux value on the boundary:
Set up the heat transfer mass transport model variables ![]() :
:
Specify heat transfer and mass transport model parameters, heat source ![]() , thermal conductivity
, thermal conductivity ![]() , mass diffusivity
, mass diffusivity ![]() and mass source
and mass source ![]() :
:
Specify boundary condition parameters for a thermal convection value with an external flow temperature ![]() of 1000 K and a heat transfer coefficient
of 1000 K and a heat transfer coefficient ![]() of
of ![]() :
:
Possible Issues (1)
For symbolic computation, the "ThermalConductivity" parameter should be given as a matrix:
For numeric values, the "ThermalConductivity" parameter is automatically converted to a matrix of proper dimensions:
This automatic conversion is not possible for symbolic input:
Not providing the properly dimensioned matrix will result in an error:
Tech Notes
Related Guides
Text
Wolfram Research (2020), HeatTransferPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html (updated 2022).
CMS
Wolfram Language. 2020. "HeatTransferPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html.
APA
Wolfram Language. (2020). HeatTransferPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_heattransferpdecomponent, author="Wolfram Research", title="{HeatTransferPDEComponent}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_heattransferpdecomponent, organization={Wolfram Research}, title={HeatTransferPDEComponent}, year={2022}, url={https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html}, note=[Accessed: 08-January-2026]}