HeatRadiationValue

HeatRadiationValue[pred,vars,pars]

represents a thermal radiation boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.

HeatRadiationValue[pred,vars,pars,lkey]

represents a thermal radiation boundary condition with local parameters specified in pars[lkey].

Details

  • HeatRadiationValue specifies a boundary condition for HeatTransferPDEComponent and is used as part of the modeling equation:
  • HeatRadiationValue is typically used to model heating or cooling through radiation on some part of the boundary. Common examples include an electrical radiator or a fireplace.
  • HeatRadiationValue models heating or cooling through radiation with dependent variable [TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]], independent variables in [TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]] and time variable in [TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]].
  • Stationary variables vars are vars={Θ[x1,…,xn],{x1,…,xn}}.
  • Time-dependent variables vars are vars={Θ[t,x1,…,xn],t,{x1,…,xn}}.
  • The non-conservative time-dependent heat transfer model HeatTransferPDEComponent is based on a convection-diffusion model with mass density , specific heat capacity 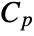, thermal conductivity 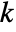, convection velocity vector and heat source :
  • The thermal radiation value HeatRadiationValue with the dimensionless emissivity, the Boltzmann constant, an ambient temperature and 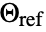a reference temperature and boundary unit normal models:
  • The emissivity is the effectiveness of a material emitting heat and can have a value in the range of .
  • Model parameters pars as specified for HeatTransferPDEComponent.
  • The following additional model parameters pars can be given:
  • parameterdefaultsymbol
    "AmbientTemperature"
  • 0
    		• , ambient temperature [TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]]
    "BoltzmannConstant", Boltzmann constant [
    "Emissivity"1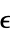
    "ReferenceTemperature"0, reference temperature [TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]]
  • The Boltzmann constant has units [] and the temperatures of the PDE model need to be specified in Kelvin.
  • The "BoltzmannConstant" parameter can only be specified in pars, not with lkey.
  • The default reference temperature is 0 Kelvin, but other units can be used after a conversion.
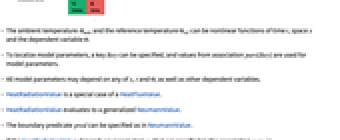
  • The ambient temperature and the reference temperature can be nonlinear functions of time , space and the dependent variable .
  • To localize model parameters, a key lkey can be specified, and values from association pars[lkey] are used for model parameters.
  • All model parameters may depend on any of , 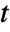and , as well as other dependent variables.
  • HeatRadiationValue is a special case of a HeatFluxValue.
  • HeatRadiationValue evaluates to a generalized NeumannValue.
  • The boundary predicate pred can be specified as in NeumannValue.
  • If the HeatRadiationValue depends on parameters that are specified in the association pars as …,keypi…,pivi,…], the parameters are replaced with .

Examples

open allclose all

Basic Examples  (2)

Set up a thermal radiation boundary condition:

Model a temperature field and a thermal radiation boundary with:

rho C_p(partialTheta(t, x))/(partialt)+del .(-k del Theta(t,x))^(︷^( heat transfer model )) =|_(Gamma_(x=0))epsilon k_B ((Theta_(amb)-Theta_(ref))^4-(Theta(t,x)-Theta_(ref))^( 4))^(︷^( heat radiation boundary ))

Set up the heat transfer model variables vars:

Set up a region :

Specify heat transfer model parameters mass density , specific heat capacity and thermal conductivity :

Specify boundary condition parameters with a constant ambient temperature of –25 °C and a surface emissivity of :

Specify the equation:

Set up initial conditions:

Solve the PDE:

Visualize the solution:

Scope  (6)

Basic Examples  (5)

Define model variables vars for a transient temperature field with model parameters pars and a specific boundary condition parameter:

Define model variables vars for a transient temperature field with model parameters pars and multiple specific parameter boundary conditions:

Set up a reference temperature of absolute zero in degrees Celsius:

Set up a thermal radiation boundary condition with a reference and ambient temperature in Celsius:

If no value for emissivity is specified, then an emissivity of 1 is assumed:

Set up a thermal radiation boundary condition with ambient temperature emissivity :

2D  (1)

Model a ceramic strip that is embedded in a high-thermal-conductive material. The side boundaries of the strip are maintained at a constant temperature . The top surface of the strip is losing heat via both heat convection and heat radiation to the ambient environment at . The bottom boundary, however, is assumed to be thermally insulated:

Model a temperature field and the thermal radiation and thermal transfer with:

del .(-k del Theta(x,y))^(︷^( heat transfer model )) =|_(Gamma_(x=0))epsilon k_B ((Theta_(amb)-Theta_(ref))^4-(Theta(x,y)-Theta_(ref))^( 4))^(︷^( heat radiation boundary ))+|_(Gamma_(x=0))h (Theta_(ext)(x,y)-Theta(x,y))^(︷^( heat transfer boundary ))

Set up the heat transfer model variables vars:

Set up a rectangular domain with a width of and a height of :

Specify thermal conductivity :

Set up temperature surface boundary conditions at the left and right boundaries:

Set up a heat transfer boundary condition on the top surface:

Also set up a thermal radiation boundary condition on the top surface:

Set up the equation:

Solve the PDE:

Visualize the solution:

Applications  (1)

Model the temperature field and a thermal radiation boundary with:

rho C_p(partialTheta(t, x))/(partialt)+del .(-k del Theta(t,x))^(︷^( heat transfer model )) =|_(Gamma_(x=0))epsilon k_B ((Theta_(amb)-Theta_(ref))^4-(Theta-Theta_(ref))^( 4))^(︷^( heat radiation boundary ))

Set up the heat transfer model variables vars:

Set up a region region:

Specify heat transfer model parameters density , specific heat capacity and thermal conductivity :

Specify boundary condition parameters with a constant ambient temperature of and a surface emissivity of :

Specify the equation:

Solve the PDE:

Visualize the solution:

Wolfram Research (2020), HeatRadiationValue, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatRadiationValue.html (updated 2022).

Text

Wolfram Research (2020), HeatRadiationValue, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatRadiationValue.html (updated 2022).

CMS

Wolfram Language. 2020. "HeatRadiationValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HeatRadiationValue.html.

APA

Wolfram Language. (2020). HeatRadiationValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatRadiationValue.html

BibTeX

@misc{reference.wolfram_2025_heatradiationvalue, author="Wolfram Research", title="{HeatRadiationValue}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HeatRadiationValue.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_heatradiationvalue, organization={Wolfram Research}, title={HeatRadiationValue}, year={2022}, url={https://reference.wolfram.com/language/ref/HeatRadiationValue.html}, note=[Accessed: 21-February-2025 ]}