HeatSymmetryValue

HeatSymmetryValue[pred,vars,pars]

represents a thermal symmetry boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.

HeatSymmetryValue[pred,vars,pars,lkey]

represents a thermal symmetry boundary condition with local parameters specified in pars[lkey].

Details

  • HeatSymmetryValue specifies a boundary condition for HeatTransferPDEComponent and is used as part of the modeling equation:
  • HeatSymmetryValue is typically used to model a boundary with mirror symmetry along an axis.
  • HeatSymmetryValue models a boundary with mirror symmetry with dependent variable in [TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]], independent variables in [TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]] and time variable in [TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]].
  • Stationary variables vars are vars={Θ[x1,…,xn],{x1,…,xn}}.
  • Time-dependent variables vars are vars={Θ[t,x1,…,xn],t,{x1,…,xn}}.
  • The non-conservative time-dependent heat transfer model HeatTransferPDEComponent is based on a convection-diffusion model with mass density , specific heat capacity , thermal conductivity , convection velocity vector and heat source :
  • The normal flow velocity on the symmetry boundary will remain at zero at all times.
  • HeatSymmetryValue with boundary unit normal models:
  • Model parameters pars as specified for HeatTransferPDEComponent.
  • The following additional model parameters pars can be given:
  • parameterdefaultsymbol
    "ModelForm""NonConservative"-
  • HeatSymmetryValue is effectively the same as HeatFluxValue with a heat flux of 0.
  • The boundary predicate pred can be specified as in NeumannValue.
  • If the HeatSymmetryValue depends on parameters that are specified in the association pars as …,keypi…,pivi,…], the parameters 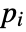are replaced with .

Examples

Basic Examples  (2)

Set up a thermal symmetry boundary condition:

Compute the temperature field with model variables vars and parameters pars:

Set up the equation with a symmetry axis at and a constant heat flux of applied on the left end:

Solve the PDE:

Visualize the solution computed in the reduced domain over the full domain:

Wolfram Research (2020), HeatSymmetryValue, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatSymmetryValue.html.

Text

Wolfram Research (2020), HeatSymmetryValue, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatSymmetryValue.html.

CMS

Wolfram Language. 2020. "HeatSymmetryValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeatSymmetryValue.html.

APA

Wolfram Language. (2020). HeatSymmetryValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatSymmetryValue.html

BibTeX

@misc{reference.wolfram_2025_heatsymmetryvalue, author="Wolfram Research", title="{HeatSymmetryValue}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/HeatSymmetryValue.html}", note=[Accessed: 13-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_heatsymmetryvalue, organization={Wolfram Research}, title={HeatSymmetryValue}, year={2020}, url={https://reference.wolfram.com/language/ref/HeatSymmetryValue.html}, note=[Accessed: 13-March-2025 ]}