HeatTemperatureCondition[pred,vars,pars]
represents a thermal surface boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
HeatTemperatureCondition[pred,vars,pars,lkey]
represents a thermal surface boundary condition with local parameters specified in pars[lkey].


HeatTemperatureCondition
HeatTemperatureCondition[pred,vars,pars]
represents a thermal surface boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
HeatTemperatureCondition[pred,vars,pars,lkey]
represents a thermal surface boundary condition with local parameters specified in pars[lkey].
Details

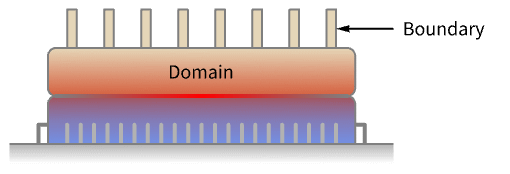
- HeatTemperatureCondition specifies a boundary condition for HeatTransferPDEComponent.
- HeatTemperatureCondition is typically used to set a specific temperature on the boundary. Common examples include the heat given off by a CPU to a heat sink.
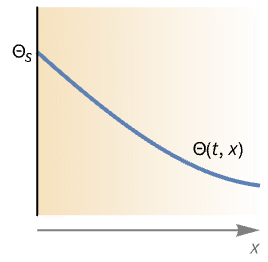
- HeatTemperatureCondition sets a specific temperature on the boundary with dependent variable
 in [
in [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTemperatureCondition.en/3.png) ], independent variables
], independent variables 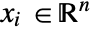 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/HeatTemperatureCondition.en/5.png) ] and time variable
] and time variable 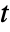 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/HeatTemperatureCondition.en/7.png) ].
]. - Stationary variables vars are vars={Θ[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={Θ[t,x1,…,xn],t,{x1,…,xn}}.
- The thermal surface condition HeatTemperatureCondition models
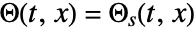 .
. - Model parameters pars are specified as for HeatTransferPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "SurfaceTemperature" - 0
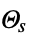 , surface temperature [
, surface temperature [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTemperatureCondition.en/11.png) ]
] - HeatTemperatureCondition evaluates to a DirichletCondition.
- The boundary predicate pred can be specified as in DirichletCondition.
- If the HeatTemperatureCondition depends on parameters
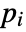 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 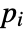 are replaced with
are replaced with 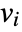 .
.
Examples
open all close allBasic Examples (2)
Scope (4)
Basic Examples (2)
1D (1)
3D (1)
Model a temperature field with two heat conditions at the sides and an orthotropic thermal conductivity ![]() :
:
Set up the heat transfer model variables ![]() :
:
Specify an orthotropic thermal conductivity ![]() :
:
Specify the heat surface conditions:
Set up the equation with a thermal heat flux ![]() of
of ![]() applied at the left end for the first 300 seconds:
applied at the left end for the first 300 seconds:
Tech Notes
Related Guides
History
Text
Wolfram Research (2020), HeatTemperatureCondition, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatTemperatureCondition.html.
CMS
Wolfram Language. 2020. "HeatTemperatureCondition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeatTemperatureCondition.html.
APA
Wolfram Language. (2020). HeatTemperatureCondition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatTemperatureCondition.html
BibTeX
@misc{reference.wolfram_2025_heattemperaturecondition, author="Wolfram Research", title="{HeatTemperatureCondition}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/HeatTemperatureCondition.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_heattemperaturecondition, organization={Wolfram Research}, title={HeatTemperatureCondition}, year={2020}, url={https://reference.wolfram.com/language/ref/HeatTemperatureCondition.html}, note=[Accessed: 24-February-2026]}