NDEigensystem

NDEigensystem[ℒ[u[x,y,…]],u,{x,y,…}∈Ω,n]

gives the n smallest magnitude eigenvalues and eigenfunctions for the linear differential operator ℒ over the region Ω.

NDEigensystem[{ℒ1[u[x,y,…],v[x,y,…],…],ℒ2[u[x,y,…],v[x,y,…],…],…},{u,v,…},{x,y,…}∈Ω,n]

gives eigenvalues and eigenfunctions for the coupled differential operators {op1,op2,…} over the region Ω.

NDEigensystem[eqns,{u,…},t,{x,y,…}∈Ω,n]

gives the eigenvalues and eigenfunctions in the spatial variables {x,y,…} for solutions u,… of the coupled time-dependent differential equations eqns.

Details and Options

  • NDEigensystem, also known as an eigenmode solver, is a numerical eigen solver that finds eigenvectors and eigenvalues of differential equations over regions.
  • NDEigensystem gives lists {{λ1,…,λn},{u1,…,un}} of eigenvalues λi and eigenfunctions ui or {{λ1,…,λn},{{u1,v1,…},…,{un,vn,…}} in case of coupled systems.
  • The equations eqns are specified as in NDSolve.
  • An eigenvalue and eigenfunction pair {λi,ui} for the differential operator ℒ satisfy ℒ[u[x,y,…]]==λi ui[x,y,…].
  • An eigenvalue and eigenfunctions pair {λi,{ui,vi,…}} for coupled differential operators satisfy:
  • ℒ1[ui[x,y,…],vi[x,y,…],…]λi ui[x,y,…]
    ℒ2[ui[x,y,…],vi[x,y,…],…]==λi vi[x,y,…]
    ⋮
  • Eigenvalues are sorted in order of increasing absolute value.
  • With the default normalization, the eigenfunctions ui computed by NDEigensystem[ℒ[u[x,y,…]],u,{x,y,…}∈Ω,n] approximately satisfy . »
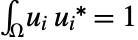  • With the default normalization, the eigenfunctions {ui,vi,…} for coupled differential operators approximately satisfy .
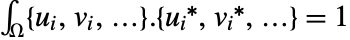  • Homogeneous DirichletCondition, NeumannValue or generalized Robin boundary conditions may be included. »
  • PeriodicBoundaryCondition may be included.
  • When no boundary condition is specified on part of the boundary ∂Ω, then this is equivalent to specifying a Neumann 0 condition.
  • For a system of first-order time-dependent equations, the time derivatives D[u[t,x,y,…],t], D[v[t,x,y,…],t],… are effectively replaced with λ u[x,y,…], λ v[x,y,…],….
  • Systems of time-dependent equations that are higher than first order are reduced to a coupled first-order system with intermediate variables ut=u*,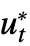=…, vt=v*,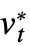=…, … Only the functions u, v, … are returned. »
  • NDEigensystem accepts a Method option that may be used to control different stages of the solution. With Method->{s1->m1,s2->m2,…}, stage si is handled by method mi. When stages are not given explicitly, NDEigensystem tries to automatically determine what stage to apply a given method to.
  • Possible solution stages are:
  • "PDEDiscretization"discretization of spatial operators
    "Eigensystem"computation of the eigensystem from the discretized system
    "Interpolation"creation of interpolating functions
    "VectorNormalization"normalization of the eigenvectors that are used to construct the eigenfunctions

Examples

open allclose all

Basic Examples  (3)

Find the 4 smallest eigenvalues and eigenfunctions of the Laplacian operator on [0,π]:

Visualize the eigenfunctions:

Compute the first 6 eigenfunctions for a circular membrane with the edges clamped:

Visualize the eigenfunctions:

Specify a Schrödinger operator with parameter and potential :

Find the 5 smallest eigenvalues and eigenfunctions:

Visualize the eigenfunctions scaled by and offset by the respective eigenvalue:

Scope  (13)

1D  (7)

Specify a Laplacian operator:

Specify homogeneous Dirichlet boundary conditions:

Find the 4 smallest eigenvalues and eigenfunctions:

Visualize the eigenfunctions:

Specify a Laplacian operator:

Specify homogeneous Neumann boundary conditions:

Find the 4 smallest eigenvalues and eigenfunctions:

This is equivalent:

Specify a transient equation with homogeneous Dirichlet boundary conditions:

Find the 4 smallest eigenvalues and eigenfunctions:

This is equivalent:

Find 5 eigenvalues and eigenvectors of a Laplacian with periodic boundary conditions:

Compare the eigenvalues with the expected analytical eigenvalues:

Visualize the eigenfunctions:

Inspect to see that the bounds are periodic:

An equivalent formulation using PeriodicBoundaryCondition:

Specify a wave equation with homogeneous Dirichlet boundary conditions:

Find the 4 smallest eigenvalues and eigenfunctions:

Compute the eigensystem of a generalized wave equation :

Compare to the exact solution of an equivalent first-order system of ordinary differential equations:

Specify a Liouville operator:

Compute the 4 smallest eigenvalues and eigenfunctions:

Compare the eigenvalues with the analytical eigenvalues:

Visualize the eigenfunctions:

Visualize the analytical eigenfunctions:

2D  (6)

Specify a Laplacian operator:

Find the 4 smallest eigenvalues and eigenfunctions:

Visualize the eigenfunctions:

Specify a Laplacian operator:

Find the 4 smallest eigenvalues and eigenfunctions of the operator in a unit disk:

Visualize the eigenfunctions:

Specify a Laplacian operator with homogeneous Dirichlet boundary conditions:

Find the 9 smallest eigenvalues and eigenfunctions in a rectangle:

Visualize the eigenfunctions:

Specify a wave equation with homogeneous Dirichlet boundary conditions:

Find the 4 smallest eigenvalues and eigenfunctions in a disk:

Visualize the eigenfunctions:

The eigenvalues of the wave equation will be the square root of the angular frequencies:

Compare to the exact solution of an equivalent first-order system of ordinary differential equations:

Solve a partially constrained eigensystem problem:

Visualize the eigenfunctions:

Options  (9)

Method  (9)

"Eigensystem"  (4)

The discretized PDE is solved with Eigensystem or Eigenvalues. All Eigensystem options available in NDEigensystem are discussed in the following.

Specify a method to use for solving the eigensystem:

In this case, the default method is faster:

Arnoldi is used as the default method:

The Arnoldi method is numerically more efficient but less stable than the direct method, which is usable only for small-scale problems.

Specify a maximum number of iterations for the Arnoldi method:

The FEAST method is suitable for finding eigenvalues and eigenvectors within a band. Find two eigenvalues and eigenfunctions of a Sturm–Liouville operator within the band of with the FEAST method for Eigensystem:

According to the Sturm–Liouville theory, the eigenvalues must be distinct, but for this example they are close to degenerate:

The almost degenerate eigenfunctions are:

The interval end points are not included in the interval FEAST finds eigenvalues in; for more information, please refer to the Eigensystem reference page.

The usage of the "Shift" option is explained in an example below.

"Interpolation"  (1)

By default, the eigenfunctions give Indeterminate for points outside the region :

Modify the default behavior to eliminate the warning messages:

Evaluate the second eigenfunction outside of the region :

Visualize part of the solution:

Change the eigenfunctions to return an extrapolated value outside of the region :

Evaluate the second eigenfunction outside of the region :

"PDEDiscretization"  (1)

Change the MaxCellMeasure for the underlying computation:

The exact eigenvalues are 0,1,4,9,…, so the eigenvalue error is as follows:

A finer mesh results in a decreased discretization error:

"VectorNormalization"  (3)

Compute without any normalization of the computed eigenvalues:

The default is to normalize with respect to the system matrices:

The functions are constructed by interpolating the eigenvectors:

NDEigensystem constructs the damping (mass) and stiffness system matrices to be solved as a generalized eigensystem. The normalization of the eigenvectors is constructed such that applying the normalized eigenvector to the damping (mass) matrix forms an identity matrix:

Applying the normalized eigenvector to the stiffness matrix produces eigenvalues on the diagonal:

With the default normalization, the L2 norm of the eigenfunctions will be approximately 1:

Degrees of freedom associated with Dirichlet conditions are removed before the eigensystem is computed, and 0 is reinserted after the solution. This results in different dimensions of the normalization vector and the eigenvector for constraint problems:

During the eigensystem computation, the two Dirichlet conditions are removed:

After the eigensystem computation, zero values are reintroduced into the functions:

Applications  (10)

Acoustics  (1)

Compute the acoustic eigenvalues and eigenfunctions for an approximation of a cross section through a Mini. Import an image of the cross section:

Use the mask tool to create a boundary graphic:

Discretize the graphic:

Compute 6 eigenvalues and eigenfunctions of the cross section:

Visualize the second eigenfunction in the cross section of the car:

The visualization shows qualitatively a standing wave assuming acoustically rigid walls. A large amplitude corresponds to a large change in pressure and thus a large acoustic volume.

Structural Mechanics  (2)

Specify a plane stress PDE:

Compute constraint eigenvalues and eigenfunctions:

Visualize the scaled norm of the eigenfunctions:

The visualization shows the principal deformation of the region.

Specify variables and parameters for a plane stress model for steel:

Compute the first eigenvalue and eigenfunction of a beam with length 10 meters and height 0.7 meters:

Compute resonant frequency from the eigenvalue:

Compute the first resonance frequency analytically utilizing Euler–Bernoulli beam theory:

Compare the difference in results; about half the difference is attributable to the different theoretical approaches:

Eigenfunction Expansions  (4)

Construct a solution for a plucked clamped string using an eigenfunction expansion:

Approximate the initial condition 1-TemplateBox[{{{2, x}, -, 1}}, Abs] as a linear combination of eigenfunctions:

Construct the time-dependent solution using the coefficients and the eigenvalues as frequencies, assuming that the time derivative at is 0:

Make an animation of the approximation, including each of the functions with nonzero coefficients:

Compare to the time-dependent solution found by NDSolve:

Make a plot of the difference:

Compare different harmonic frequencies on a circular drum:

Show a time evolution for each of the eigenfunctions over one cycle of the first:

Reduce the size of the graphics:

Note that the eigenfunctions with larger eigenvalues oscillate more quickly:

Show the time evolution of a linear combination of eigenfunctions:

This is the solution of the wave equation with consistent initial conditions:

Show the difference between a finite eigenexpansion and full solution:

Use an eigenfunction expansion to get a solution of the heat equation on a region:

Compute the first 20 eigenvalues and eigenfunctions for the Laplacian on :

Let be an initial condition:

For computing integrals, it is faster and more consistent to use the discretized domain Ωd:

Since does not satisfy the homogeneous boundary conditions, find the steady state solution that does on the discretized domain Ωd, so that does satisfy them:

Compute the coefficients of the eigenfunction expansion for the difference :

The approximation to the solution of the heat equation is as follows:

Compute the time-dependent solution:

Make a plot of the difference:

Eigenfunctions in an L-shaped region:

The first six eigenfunctions:

The first one:

Interval of Eigenvalues and Eigenfunctions  (1)

Find an eigenvalue and a eigenfunction in an interval:

Visualize the eigenfunction found:

Quantum Mechanics  (2)

Specify a Schrödinger operator with parameter and potential :

Find the 10 smallest eigenvalues and eigenfunctions on a refined mesh:

Visualize the eigenfunctions scaled by and offset by the respective eigenvalue:

This example shows the avoided-crossing phenomenon of eigenvalues. For this, a region difference between two disks is computed The outer disk has a radius of and its center is at . The inner disk has a radius of . The center of the inner disk starts from the central position and slowly moves to the right by . Write a helper function:

Compute the eigenvalues and vectors:

Visualize the eigenvalues of the Laplacian of the geometry at the various positions of :

Note that some curves cross, while others show an avoided-crossing phenomenon.

Visualize the eigenvectors for a particular solution:

Properties & Relations  (3)

With the default normalization, the eigenfunctions ui approximately satisfy :

When the eigenvalues are complex, it is necessary to use the conjugate:

Compare the approximated eigensystem to one computed analytically for the wave equation.

Find the 6 smallest eigenvalues and eigenfunctions of a wave equation within 0 and :

The eigenvalues of the PDE system converted to first order in time correspond to eigenvalues of the matrix , where is an eigenvalue of with at the boundaries:

Show the relationship between higher-order time-dependent PDEs and systems of first-order PDEs.

Find the 6 smallest eigenvalues and eigenfunctions of the wave equation within 0 and :

Plot the modulus and the real and imaginary parts of the eigenfunctions:

Find the 6 smallest eigenvalues and eigenfunctions of a wave equation given as a system of first-order PDEs :

Plot the modulus and the real and imaginary parts of the eigenfunctions:

The eigenvalues for the second-order system and the system of first-order equations are the same:

For a given eigenvalue, the eigenfunction returned for the second-order system is the same as the first eigenfunction returned for the system:

For a given eigenvalue, times the eigenfunction returned for the second-order system is the same as the second eigenfunction returned for the system:

The eigenfunctions for the system are normalized so that :

The eigenfunctions for the second-order time-dependent system are normalized in the same way as the system, and since , int_Omega{u_i,v_i,...}.{u_i,v_i,...}=(1+lambda_i^2)int_OmegaTemplateBox[{{u, _, i}}, Abs]^2=1 so int_OmegaTemplateBox[{{u, _, i}}, Abs]^2=1/((1+lambda_i^2)):

Possible Issues  (15)

The computed eigensystem depends on the granularity of the discretization:

The exact eigenvalues are 0,1,4,9,…, so the eigenvalue error is as follows:

Visualize the discretization error in -TemplateBox[{{(, {u, , x}, )}, {{, x, }}}, Laplacian]=lambda (u x):

A finer mesh results in a decreased discretization error:

Visualize the discretization error in :

The granularity of the discretization of the region influences the number of eigenvalues and eigenfunctions that can be found:

The differences between the eigenvalues and eigenfunctions in a coarser versus a finer discretization tend to increase with the mode number:

Eigensystems with inhomogeneous Dirichlet conditions cannot be solved:

Eigensystems with homogeneous Dirichlet conditions can be solved:

Eigensystems with inhomogeneous Neumann values cannot be solved:

Eigensystems with homogeneous Neumann values can be solved:

The same result:

Eigensystems with inhomogeneous generalized Neumann values cannot be solved:

Eigensystems with homogeneous generalized Neumann values can be solved:

The operator and possible boundary conditions need to be stationary and linear:

Initial conditions will be set to zero and ignored:

The same result:

The eigenvalues and eigenfunctions will be sorted by magnitude. Define a potential function:

Note the negative eigenvalues:

Obtain the eigenvalues by the real part:

NDEigensystem finds the smallest magnitude eigenvalues and their correspondent eigenfunctions for a given differential operator. Particularly in cases where one is interested in finding the most negative eigenvalues, e.g. many quantum mechanical problems, the most negative eigenvalues might not correspond with the eigenvalues NDEigensystem returns by default. To see this, consider the following example.

Take, for instance, the dimensionless radial Schrödinger equation for the hydrogen atom, where the energy units are Rydbergs and length is measured in Bohr radii.

Define the radial Schrödinger equation:

Solve the eigenvalue problem for . A refined mesh is used for a good approximation quality:

Look at the eigenvalues obtained in electronvolts:

These correspond to the eigenvalues closest to . But they are not in the desired order. For instance, take a look at the analytical eigenvalues for this problem.

The analytical energies for this equation follow this equation:

If you know in advance a lower bound for the eigenvalues, say , you can redefine the eigenvalue problem as . In other words, a new eigenvalue problem: , where and . Given that is a negative lower bound for , the shift ensures that will only assume positive values. Therefore, the smallest magnitude values of will correspond to the most negative values of . That way, one can calculate for and then get . The easiest way to do this is to use the "Shift" option.

Set a lower bound:

Define a shift and solve the eigenvalue problem:

Look at the eigenvalues obtained in electronvolts:

These correspond to the most negative eigenvalues, but in reverse order, and then it is necessary to sort the eigenstates.

Sort the eigenstates with SortBy:

Plot the probability densities:

Take a look at the difference between the analytical eigenvalues and the obtained results:

NDEigensystem converts PDEs to time-dependent PDEs. This transformation is not unique and may lead to what seem to be unexpected results for coupled PDEs:

Internally, the given equations are rewritten as a system of time-dependent PDEs. This is done by adding time-dependent derivative terms and a time variable to the operator and setting them to 0. In the previous case, from the given dependent variables {v[x],u[x]}, the following temporal system is generated: {D[v[t,x],t]==- u[t,x]-Laplacian[u[t,x],{x}],D[u[t,x],t]==-v[t,x]-Laplacian[v[t,x],{x}]}

Because of the ordering of the dependent variables {v[x],u[x]}, the first equation has a time derivative term on v[t,x] and the second equation has a time derivative term on u[t,x]. This is most likely not the intended equation.

To uniquely specify the system of equations, it is best to use the temporal description:

As an alternative, the dependent variables can be given in the order {u[x],v[x]}:

More information on this topic can be found in Finite Element Method Usage Tips.

Caution needs to be exercised when converting equations. Consider the Sturm–Liouville problem with homogeneous Dirichlet conditions. The analytical solution of the eigenvalues is given by:

To avoid numerical stability problems at , it is best to use the temporal description:

Compare this to the following formulation of the problem:

In some cases, NDEigensystem may return what seem to be unexpected results for coupled PDEs:

One way to avoid this issue is to specify an ordering of the dependent variables via the "InterpolationOrder" option:

Alternatively, the "Direct" method can be used:

More information on this topic can be found in Finite Element Method Usage Tips.

Eigenfunctions can be negative multiples of an analytical solution.

Define parameters for an eigenvalue problem with an analytical solution:

Solve the eigensystem:

Compare the analytical to the numerical eigenfunction, which differ by a multiplicative :

There is no overall sign guaranteed for the eigenfunctions; () times an eigenfunction is still an eigenfunction. In fact, any constant times an eigenfunction is still an eigenfunction. NDEigensystem chooses eigenfunctions that have a unit norm, as explained in the properties and relations section.

Currently, NDEigensystem cannot deal with indexed variables:

Construct a list of dependent variables:

When integrating over the eigenfunctions, NIntegrate may have a hard time when using symbolic regions:

While the result is correct, it may be more efficient to use the same mesh that was used for the numerical eigensystem computation:

Neat Examples  (1)

Explore how eigenfunctions in this quantum mechanics example tend to cluster when the number of wells increases and in the infinite space limit form allowed energy bands. At the same time, the influence of the boundary conditions decreases with increasing structure size. Also note that within a band the eigenfunctions are quite different (they must be orthogonal to each other), while the squared eigenfunctions are similar. This indicates the various possibilities to form superpositions from the approximate eigenfunctions of a single well:

Wolfram Research (2015), NDEigensystem, Wolfram Language function, https://reference.wolfram.com/language/ref/NDEigensystem.html (updated 2023).

Text

Wolfram Research (2015), NDEigensystem, Wolfram Language function, https://reference.wolfram.com/language/ref/NDEigensystem.html (updated 2023).

CMS

Wolfram Language. 2015. "NDEigensystem." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/NDEigensystem.html.

APA

Wolfram Language. (2015). NDEigensystem. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NDEigensystem.html

BibTeX

@misc{reference.wolfram_2024_ndeigensystem, author="Wolfram Research", title="{NDEigensystem}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/NDEigensystem.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ndeigensystem, organization={Wolfram Research}, title={NDEigensystem}, year={2023}, url={https://reference.wolfram.com/language/ref/NDEigensystem.html}, note=[Accessed: 21-November-2024 ]}