Eigenvalues

Eigenvalues[m]

gives a list of the eigenvalues of the square matrix m.

Eigenvalues[{m,a}]

gives the generalized eigenvalues of m with respect to a.

Eigenvalues[m,k]

gives the first k eigenvalues of m.

Eigenvalues[{m,a},k]

gives the first k generalized eigenvalues.

Details and Options

  • Eigenvalues finds numerical eigenvalues if m contains approximate real or complex numbers.
  • Repeated eigenvalues appear with their appropriate multiplicity.
  • An 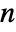× 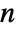matrix gives a list of exactly 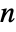eigenvalues, not necessarily distinct.
  • If they are numeric, eigenvalues are sorted in order of decreasing absolute value.
  • The eigenvalues of a matrix m are those 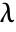for which 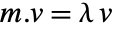for some nonzero eigenvector . »
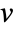  • The finite generalized eigenvalues of m with respect to a are those 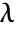for which . »
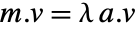  • Ordinary eigenvalues are always finite; generalized eigenvalues can be infinite.
  • When matrices m and a have a dimension‐ 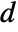shared null space, then 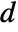of their generalized eigenvalues will be Indeterminate. »
  • For numeric eigenvalues, Eigenvalues[m,k] gives the k that are largest in absolute value.
  • Eigenvalues[m,-k] gives the k that are smallest in absolute value.
  • Eigenvalues[m,spec] is always equivalent to Take[Eigenvalues[m],spec].
  • Eigenvalues[m,UpTo[k]] gives k eigenvalues, or as many as are available.
  • SparseArray objects and structured arrays can be used in Eigenvalues.
  • Eigenvalues has the following options and settings:
  • Cubics Falsewhether to use radicals to solve cubics
    Method Automaticmethod to use
    Quartics Falsewhether to use radicals to solve quartics
  • Explicit Method settings for approximate numeric matrices include:
  • "Arnoldi"Arnoldi iterative method for finding a few eigenvalues
    "Banded"direct banded matrix solver for Hermitian matrices
    "Direct"direct method for finding all eigenvalues
    "FEAST"FEAST iterative method for finding eigenvalues in an interval (applies to Hermitian matrices only)
  • The "Arnoldi" method is also known as a Lanczos method when applied to symmetric or Hermitian matrices.
  • The "Arnoldi" and "FEAST" methods take suboptions Method->{"name",opt1->val1,…}, which can be found in the Method subsection.

Examples

open allclose all

Basic Examples  (4)

Machine-precision numerical eigenvalues:

Eigenvalues of an arbitrary-precision matrix:

Eigenvalues of an exact matrix:

Symbolic eigenvalues:

Scope  (19)

Basic Uses  (6)

Find the eigenvalues of a machine-precision matrix:

Approximate 20-digit precision eigenvalues:

Eigenvalues of a complex matrix:

Exact eigenvalues:

The eigenvalues of large numerical matrices are computed efficiently:

Eigenvalues of a CenteredInterval matrix:

Find the eigenvalues for a random representative mrep of m:

Verify that, after reordering, vals contain rvals:

Subsets of Eigenvalues  (5)

The largest five eigenvalues:

Three smallest eigenvalues:

Find the four largest eigenvalues, or as many as there are if fewer:

Repeated eigenvalues are listed multiple times:

Repeats are considered when extracting a subset of the eigenvalues:

Generalized Eigenvalues  (4)

Generalized machine-precision eigenvalues:

Generalized exact eigenvalues:

Compute the result at finite precision:

Find the generalized eigenvalues of symbolic matrices:

Find the two smallest generalized eigenvalues:

Special Matrices  (4)

Eigenvalues of sparse matrices:

Eigenvalues of structured matrices:

IdentityMatrix always has all-one eigenvalues:

Eigenvalues of HilbertMatrix:

Options  (10)

Cubics  (1)

Eigenvalues uses Root to compute exact eigenvalues:

Explicitly use the cubic formula to get the result in terms of radicals:

Method  (8)

"Arnoldi"  (5)

The Arnoldi method can be used for machine- and arbitrary-precision matrices. The implementation of the Arnoldi method is based on the "ARPACK" library. It is most useful for large sparse matrices.

The following options can be specified for the method "Arnoldi":

  • "BasisSize"the size of the Arnoldi basis
    "Criteria"which criteria to use
    "MaxIterations"
  • the maximum number of iterations
    • "Shift"
  • the Arnoldi shift
    • "StartingVector"
  • the initial vector to start iterations
    • "Tolerance"the tolerance used to terminate iterations

    • Possible settings for "Criteria" include:

  • "Magnitude"based on Abs
    "RealPart"based on Re
    "ImaginaryPart"based on Im
    "BothEnds"a few eigenvalues from both ends of the symmetric real matrix spectrum

    • Compute the largest eigenvalue using different "Criteria" settings. The matrix m has eigenvalues :

    By default, "Criteria"->"Magnitude" selects a largest-magnitude eigenvalue:

    Find the largest real-part eigenvalues:

    Find the largest imaginary-part eigenvalue:

    Find two eigenvalues from both ends of the matrix spectrum:

    Use "StartingVector" to avoid randomness:

    Different starting vectors may converge to different eigenvalues:

    Use "Shift"->μ to shift the eigenvalues by transforming the matrix to . This preserves the eigenvectors but changes the eigenvalues by -μ. The method compensates for the changed eigenvalues. "Shift" is typically used to find eigenpairs where there is no criteria such as largest or smallest magnitude that can select them:

    Manually shift the matrix and adjust the resulting eigenvalue:

    Automatically shift and adjust the eigenvalue:

    "Banded"  (1)

    The banded method can be used for real symmetric or complex Hermitian machine-precision matrices. The method is most useful for finding all eigenvalues.

    Compute the two largest eigenvalues for a banded matrix:

    "FEAST"  (2)

    The FEAST method can be used for real symmetric or complex Hermitian machine-precision matrices. The method is most useful for finding eigenvalues in a given interval.

    The following suboptions can be specified for the method "FEAST":

  • "ContourPoints"select the number of contour points
    "Interval"interval for finding eigenvalues
    "MaxIterations"the maximum number of refinement loops
    "NumberOfRestarts"the maximum number of restarts
    "SubspaceSize"the initial size of subspace
    "Tolerance"the tolerance to terminate refinement
    "UseBandedSolver"whether to use a banded solver

    • Compute eigenvalues in the interval :

    Use "Interval" to specify the interval:

    The interval endpoints are not included in the interval in which FEAST finds eigenvalues.

    Quartics  (1)

    A 4×4 matrix:

    In general, for a 4×4 matrix, the result will be given in terms of Root objects:

    You can get the result in terms of radicals using the Cubics and Quartics options:

    Applications  (15)

    The Geometry of Eigenvalues  (3)

    Eigenvectors with positive eigenvalues point in the same direction when acted on by the matrix:

    Eigenvectors with negative eigenvalues point in the opposite direction when acted on by the matrix:

    Consider the following matrix and its associated quadratic form q=TemplateBox[{x}, Transpose].a.x:

    The eigenvectors are the axes of the hyperbolas defined by :

    The sign of the eigenvalue corresponds to the sign of the right-hand side of the hyperbola equation:

    Here is a positive-definite quadratic form in three dimensions:

    Plot the surface :

    Get the symmetric matrix for the quadratic form, using CoefficientArrays:

    Numerically compute its eigenvalues and eigenvectors:

    Show the principal axes of the ellipsoid:

    Diagonalization  (4)

    Diagonalize the following matrix as m=p.d.TemplateBox[{p}, Inverse]. First, compute 's eigenvalues:

    Construct a diagonal matrix from the eigenvalues:

    Next, compute 's eigenvectors and place them in the columns of a matrix:

    Confirm the identity m=p.d.TemplateBox[{p}, Inverse]:

    Any function of the matrix can now be computed as f(m)=p.f(d).TemplateBox[{p}, Inverse]. For example, MatrixPower:

    Similarly, MatrixExp becomes trivial, requiring only exponentiating the diagonal elements of :

    Let be the linear transformation whose standard matrix is given by the matrix . Find a basis for TemplateBox[{}, Reals]^4 with the property that the representation of in that basis is diagonal:

    Find the eigenvalues of :

    Let consist of the eigenvectors, and let be the matrix whose columns are the elements of :

    converts from -coordinates to standard coordinates. Its inverse converts in the reverse direction:

    Thus is given by TemplateBox[{b}, Inverse].a.b, which is diagonal:

    Note that this is simply the diagonal matrix whose entries are the eigenvalues:

    A real-valued symmetric matrix is orthogonally diagonalizable as s=o.d.TemplateBox[{o}, Transpose], with diagonal and real valued and orthogonal. Verify that the following matrix is symmetric and then diagonalize it:

    Computing the eigenvalues, they are real, as expected:

    The matrix has the eigenvalues on the diagonal:

    Next, compute the eigenvectors of :

    For an orthogonal matrix, it is necessary to normalize the eigenvectors before placing them in columns:

    Verify that s=o.d.TemplateBox[{o}, Transpose]:

    A matrix is called normal if TemplateBox[{n}, ConjugateTranspose].n=n.TemplateBox[{n}, ConjugateTranspose]. Normal matrices are the most general kind of matrix that can be diagonalized by a unitary transformation. All real symmetric matrices are normal because both sides of the equality are simply :

    Show that the following matrix is normal, then diagonalize it:

    Confirm using NormalMatrixQ:

    The eigenvalues of a real normal matrix that is not also symmetric are complex valued:

    Construct a diagonal matrix from the eigenvalues:

    Compute the eigenvectors:

    Normalizing the eigenvectors and putting them in columns gives a unitary matrix:

    Confirm the diagonalization n=u.d.TemplateBox[{u}, ConjugateTranspose]:

    Differential Equations and Dynamical Systems  (4)

    Solve the system of ODEs , , . First, construct the coefficient matrix for the right-hand side:

    Find the eigenvalues and eigenvectors:

    Construct a diagonal matrix whose entries are the exponential of :

    Construct the matrix whose columns are the corresponding eigenvectors:

    The general solution is p.d.TemplateBox[{p}, Inverse].{TemplateBox[{1}, CTraditional],TemplateBox[{2}, CTraditional],TemplateBox[{3}, CTraditional]} for three arbitrary starting values:

    Verify the solution using DSolveValue:

    Suppose a particle is moving in a planar force field and its position vector satisfies and , where and are as follows. Solve this initial value problem for :

    First, compute the eigenvalues and corresponding eigenvectors of :

    The general solution of the system is . Use LinearSolve to determine the coefficients:

    Construct the appropriate linear combination of the eigenvectors:

    Verify the solution using DSolveValue:

    Produce the general solution of the dynamical system when is the following stochastic matrix:

    Find the eigenvalues and eigenvectors, using Chop to discard small numerical errors:

    The general solution is an arbitrary linear combination of terms of the form :

    Verify that satisfies the dynamical equation up to numerical rounding:

    The Lorenz equations:

    Find the Jacobian for the right-hand side of the equations:

    Find the equilibrium points:

    Find the eigenvalues and eigenvectors of the Jacobian at the one in the first octant:

    A function that integrates backward from a small perturbation of pt in the direction dir:

    Show the stable curve for the equilibrium point on the right:

    Find the stable curve for the equilibrium point on the left:

    Show the stable curves along with a solution of the Lorenz equations:

    Physics  (4)

    In quantum mechanics, states are represented by complex unit vectors and physical quantities by Hermitian linear operators. The eigenvalues represent possible observations and the squared modulus of the components with respect to eigenvectors the probabilities of those observations. For the spin operator and state given, find the possible observations and their probabilities:

    Computing the eigenvalues, the possible observations are :

    Find the eigenvectors and normalize them in order to compute proper projections:

    The relative probabilities are for and for :

    In quantum mechanics, the energy operator is called the Hamiltonian , and a state with energy evolves according to the Schrödinger equation . Given the Hamiltonian for a spin-1 particle in constant magnetic field in the direction, find the state at time of a particle that is initially in the state representing :

    Computing the eigenvalues, the energy levels are and :

    Find and normalize the eigenvectors:

    The state at time is the sum of each eigenstate evolving according to the Schrödinger equation:

    The moment of inertia is a real symmetric matrix that describes the resistance of a rigid body to rotating in different directions. The eigenvalues of this matrix are called the principal moments of inertia, and the corresponding eigenvectors (which are necessarily orthogonal) the principal axes. Find the principal moments of inertia and principal axis for the following tetrahedron:

    First compute the moment of inertia:

    The principle moments are the eigenvalues of :

    The principle axes are the eigenvectors of :

    Verify that the axes are orthogonal:

    The center of mass of the tetrahedron is at the origin:

    Visualize the tetrahedron and its principal axes:

    A generalized eigensystem can be used to find normal modes of coupled oscillations that decouple the terms. Consider the system shown in the diagram:

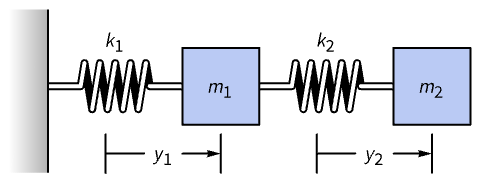
    By Hooke's law it obeys , . Substituting in the generic solution gives rise to the matrix equation , with the stiffness matrix and mass matrix as follows:

    Find the eigenfrequencies and normal modes if , , and :

    Compute the generalized eigenvalues of with respect to :

    The eigenfrequencies are the square roots of the eigenvalues:

    The shapes of the modes are derived from the generalized eigenvectors:

    Construct the normal mode solutions as a generalized eigenvector times the corresponding exponential:

    Verify that both satisfy the differential equation for the system:

    Properties & Relations  (15)

    Eigenvalues[m] is effectively the first element of the pair returned by Eigensystem:

    If both eigenvectors and eigenvalues are needed, it is generally more efficient to just call Eigensystem:

    The eigenvalues are the roots of the characteristic polynomial:

    Compute the polynomial with CharacteristicPolynomial:

    Verify the equality:

    The generalized characteristic polynomial is given by TemplateBox[{{a, -, {b, , lambda}}}, Det]:

    The generalized characteristic polynomial defines the finite eigenvalues only:

    Infinite generalized eigenvalues correspond to eigenvectors of for which :

    The product of the eigenvalues of m equals Det[m]:

    The sum of the eigenvalues of m equals Tr[m]:

    If has all distinct eigenvalues, DiagonalizableMatrixQ[m] gives True:

    The converse is false:

    For an invertible matrix , the eigenvalues of TemplateBox[{m}, Inverse] are the reciprocals of the eigenvalues of :

    Because Eigenvalues sorts by absolute value, this gives the same values but in the opposite order:

    For an analytic function , the eigenvalues of are the result of applying to the eigenvalues of :

    For example, the eigenvalues of are :

    Similarly, the eigenvalues of are :

    The eigenvalues of a real symmetric matrix are real:

    So are the eigenvalues of any Hermitian matrix:

    The eigenvalues of a real antisymmetric matrix are imaginary:

    So are the eigenvalues of any antihermitian matrix:

    The eigenvalues of an orthogonal matrix lie on the unit circle:

    So do the eigenvalues of any unitary matrix:

    SingularValueList[m] equals the square root of the nonzero eigenvalues TemplateBox[{m}, ConjugateTranspose].m:

    Consider a matrix m with a complete set of eigenvectors:

    JordanDecomposition[m] returns matrices {s,j} built from eigenvalues and eigenvectors:

    The j matrix is diagonal with eigenvalue entries, possibly in a different order than from Eigensystem:

    SchurDecomposition[n,RealBlockDiagonalFormFalse] for a numerical normal matrix n:

    The t matrix is diagonal and with eigenvalue entries, possibly in a different order from Eigensystem:

    If matrices share a dimension‐ null space, of their generalized eigenvalues will be Indeterminate:

    Two generalized eigenvalues of with respect to itself are Indeterminate:

    The matrix has a one-dimensional null space:

    It lies in the null space of of :

    Thus, one generalized eigenvalue of with respect to is Indeterminate:

    Possible Issues  (5)

    Eigenvalues and Eigenvectors are not absolutely guaranteed to give results in corresponding order:

    The sixth and seventh eigenvalues are essentially equal and opposite:

    In this particular case, the seventh eigenvector does not correspond to the seventh eigenvalue:

    Instead it corresponds to the sixth eigenvalue:

    Use Eigensystem[mat] to ensure corresponding results always match:

    The general symbolic case very quickly gets very complicated:

    The expression sizes increase faster than exponentially:

    Here is a 20×20 Hilbert matrix:

    Compute the smallest eigenvalue exactly and give its numerical value:

    Compute the smallest eigenvalue with machine-number arithmetic:

    The smallest eigenvalue is not significant compared to the largest:

    Use sufficient precision for the numerical computation:

    When eigenvalues are closely grouped, the iterative method for sparse matrices may not converge:

    The iteration has not converged well after 1000 iterations:

    You can give the algorithm a shift near the expected value to speed up convergence:

    The endpoints given to an interval as specified for the FEAST method are not included. Set up a matrix with eigenvalues at 3 and 9:

    Computing the eigenvalues in the interval does not return the values at the endpoints:

    Enlarge the interval to so that FEAST finds the eigenvalues 3 and 9:

    Wolfram Research (1988), Eigenvalues, Wolfram Language function, https://reference.wolfram.com/language/ref/Eigenvalues.html (updated 2024).

    Text

    Wolfram Research (1988), Eigenvalues, Wolfram Language function, https://reference.wolfram.com/language/ref/Eigenvalues.html (updated 2024).

    CMS

    Wolfram Language. 1988. "Eigenvalues." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Eigenvalues.html.

    APA

    Wolfram Language. (1988). Eigenvalues. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Eigenvalues.html

    BibTeX

    @misc{reference.wolfram_2025_eigenvalues, author="Wolfram Research", title="{Eigenvalues}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Eigenvalues.html}", note=[Accessed: 05-July-2025 ]}

    BibLaTeX

    @online{reference.wolfram_2025_eigenvalues, organization={Wolfram Research}, title={Eigenvalues}, year={2024}, url={https://reference.wolfram.com/language/ref/Eigenvalues.html}, note=[Accessed: 05-July-2025 ]}