Eigenvalues

Eigenvalues[m]

给出方阵 m 的特征值构成的列表.

Eigenvalues[{m,a}]

给出矩阵 m 的关于 a 的广义特征值.

Eigenvalues[m,k]

给出矩阵 m 的前 k 个特征值.

Eigenvalues[{m,a},k]

给出前 k 个广义特征值.

更多信息和选项

  • 如果 m 包含近似实、复数，Eigenvalues 求出数值特征值.
  • 特征值按重数重复出现.
  • 一个 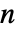× 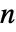矩阵给出恰好 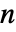个特征值，可以重复，而不必是不同的数值.
  • 特征值依绝对值递减排列.
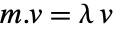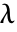  • 矩阵 m 的特征值为满足 的 （其中 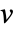为某些非零特征向量）. »
  • 关于 a 的矩阵 m 的无限广义特征值是满足 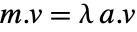的 . »
  • 普通特征值一般为有限值，广义特征值可以为无限值.
  • 矩阵 m 和 a 有 维共享空间，则 的值为 Indeterminate. »
  • 对于数值特征值，Eigenvalues[m,k] 给出绝对值最大的 k.
  • Eigenvalues[m,-k] 给出绝对值最小的 k.
  • Eigenvalues[m,spec] 等同于 Take[Eigenvalues[m],spec].
  • Eigenvalues[m,UpTo[k]] 给出 k 个特征值，如果个数不足，则尽可能多的给出特征值.
  • 可在 Eigenvalues 中使用 SparseArray 对象和结构化数组.
  • Eigenvalues 具有下列选项和设置：
  • Cubics False是否使用根式求解三次曲线
    Method Automatic选择使用的方法
    Quartics False是否使用根式求解四次曲线
  • 近似数值矩阵的显式 Method 设置包括：
  • "Arnoldi"Arnoldi 迭代方法，以求解一些特征值
    "Banded"厄米特矩阵的带状矩阵直接求解器 (direct banded matrix solver)
    "Direct"求解所有特征值的直接方法
    "FEAST"FEAST 迭代方法，以求解某区间内的特征值（只应用于 Hermitian 矩阵）
  • 当应用于对称或 Hermitian 矩阵时，"Arnoldi" 方法也称为 Lanczos 方法.
  • "Arnoldi" 和 "FEAST" 方法使用子选项 Method ->{"name",opt1->val1,…}，它可以在 Method 子章节中找到.

范例

打开所有单元关闭所有单元

基本范例  (4)

机器精度数值特征值：

任意精度矩阵的特征值：

精确矩阵的特征值：

符号特征值：

范围  (19)

基本用法  (6)

求机器精度矩阵的特征值：

近似的 20 位精度的特征值：

复矩阵的特征值：

精确的特征值：

高效计算大型数值矩阵的特征值：

CenteredInterval 矩阵的特征值：

求 m 的随机代表 mrep 的特征值：

验证重新排序后，vals 包含 rvals：

特征值的子集  (5)

五个最大的特征值：

三个最小的特征值：

求四个最大的特征值，如果没有那么多，则有多少给出多少：

列出重复的特征值：

提取特征值的子集时考虑重复的特征值：

广义的特征值  (4)

机器精度的广义特征值：

广义的精确特征值：

以有限的精度计算结果：

计算符号矩阵的广义特征值：

求两个最小的广义特征值：

特殊矩阵  (4)

稀疏矩阵的特征值：

结构化矩阵的特征值：

IdentityMatrix 的特征值全部是 1：

HilbertMatrix 的特征值：

选项  (10)

Cubics  (1)

Eigenvalues 使用 Root 计算精确特征值：

显式使用立方公式以根式形式的结果：

Method  (8)

"Arnoldi"  (5)

Arnoldi 方法可用于机器和任意精度矩阵. Arnoldi 方法的实现基于 "ARPACK" 程序库. 它对于大型稀疏矩阵很有用.

方法 "Arnoldi" 可以知道下列子选项：

  • "BasisSize"the size of the Arnoldi basis
    "Criteria"which criteria to use
    "MaxIterations"
  • the maximum number of iterations
    • "Shift"
  • the Arnoldi shift
    • "StartingVector"
  • the initial vector to start iterations
    • "Tolerance"the tolerance used to terminate iterations

    • "Criteria" 的可能设置包括：

  • "Magnitude"based on Abs
    "RealPart"based on Re
    "ImaginaryPart"based on Im
    "BothEnds"a few eigenvalues from both ends of the symmetric real matrix spectrum

    • 使用不同的 "Criteria" 设置，计算最大特征向量. 矩阵 m 具有特征值 :

    默认情况下，"Criteria"->"Magnitude" 选择对应于最大幅度特征对：

    求最大实部特征值：

    求最大虚部特征值：

    求来自对称矩阵谱两端的两个特征值：

    使用 "StartingVector" 避免随机性：

    不同的初始向量可能收敛到不同的特征值：

    使用 "Shift"->μ 通过将矩阵 变换为 平移特征值. 这保持了特征向量，但是将特征值改变了 -μ. 方法对变化了的特征值进行补偿. "Shift" 通常用于求没有选择最大或者最小幅度的标准的特征对：

    手动平移矩阵，以调整所得的特征值：

    自动平移，并且调整特征值：

    "Banded"  (1)

    带状方法可用于实对称或复厄米特机器精度矩阵. 该方法对于求出所有特征值最有用.

    计算带状矩阵的两个最大的特征值：

    "FEAST"  (2)

    FEAST 方法可用于实对称或者复 Hermitian 机器精度矩阵. 方法对于在给定区间内求特征值很有用.

    方法 "FEAST" 可以指定下列子选项：

  • "ContourPoints"select the number of contour points
    "Interval"interval for finding eigenvalues
    "MaxIterations"the maximum number of refinement loops
    "NumberOfRestarts"the maximum number of restarts
    "SubspaceSize"the initial size of subspace
    "Tolerance"the tolerance to terminate refinement
    "UseBandedSolver"whether to use a banded solver

    • 计算对应于来自区间 的特征值的特征向量：

    用 "Interval" 指定区间：

    FEAST 求特征值的区间不包括区间 的端点.

    Quartics  (1)

    4×4矩阵：

    一般来说，对于4×4矩阵，结果以 Root 对象的形式给出：

    您可以使用 Cubics 和 Quartics 选项获取以根式表示的结果：

    应用  (15)

    特征值的几何学  (3)

    当被矩阵作用时，具有正特征值的特征向量指向相同的方向：

    当被矩阵作用时，具有负特征值的特征向量指向相反的方向：

    思考以下矩阵 及其相关的二次形式 q=TemplateBox[{x}, Transpose].a.x：

    特征向量是由 定义的双曲线的轴：

    特征值的符号对应双曲线方程右侧的符号：

    这是三个维度中的正定二次形式：

    绘制曲面 ：

    使用 CoefficientArrays 获得二次式的对称矩阵：

    数值计算其特征值和特征向量：

    显示椭圆体的主轴：

    对角化  (4)

    将以下矩阵对角化为 m=p.d.TemplateBox[{p}, Inverse]. 首先，计算 的特征值：

    根据特征值构建对角矩阵 ：

    接下来，计算 的特征向量并将其放置于矩阵的列中：

    验证恒等式 m=p.d.TemplateBox[{p}, Inverse]：

    矩阵的任何函数可以 f(m)=p.f(d).TemplateBox[{p}, Inverse] 形式计算. 例如，MatrixPower：

    同样，只需要对 的对角线元素求幂即可使 MatrixExp 变为平凡：

    令 为其标准矩阵由矩阵 给出的线性变换. 求 TemplateBox[{}, Reals]^4 的基 ，其性质为 在该基 中的表示为对角线矩阵：

    求 的特征值：

    设 由特征向量组成，设 为矩阵，其列是 的元素：

    从 坐标转换为标准坐标. 其逆矩阵变换为反方向：

    因此 由 TemplateBox[{b}, Inverse].a.b 给出，为对角线矩阵：

    请注意这只是对角矩阵，其项为特征值：

    实值对称矩阵可正交对角化为 s=o.d.TemplateBox[{o}, Transpose]，其中 为实对角矩阵且 为正交矩阵. 验证以下矩阵是否对称，并进行对角化：

    计算特征值，结果如预期所想是实数：

    矩阵 在对角线上具有特征值：

    接下来，计算 的特征向量：

    对于正交矩阵，需要在将特征向量放入列之前正规化：

    验证 s=o.d.TemplateBox[{o}, Transpose]：

    如果 TemplateBox[{n}, ConjugateTranspose].n=n.TemplateBox[{n}, ConjugateTranspose]，则矩阵称为正规矩阵. 正规矩阵是可以通过酉变换进行对角化的最通用的矩阵类型. 所有实对称矩阵 都是正规矩阵，因为等式的两边都仅为 ：

    证明下面的矩阵是正规矩阵，并对其对角化：

    使用 NormalMatrixQ 进行验证：

    非对称实正规矩阵的特征值是复值：

    根据特征值构造对角矩阵：

    计算特征向量：

    对特征向量进行正规化并将其放置于列中会得到酉矩阵：

    验证对角化 n=u.d.TemplateBox[{u}, ConjugateTranspose]：

    微分方程和动力系统  (4)

    求解常微分方程 (ODE) 方程组 , , . 首先，构造右侧的系数矩阵 ：

    求特征值和特征向量：

    构造一个对角矩阵，其项是 的指数：

    构造其列是对应特征向量的矩阵：

    三个任意起始值的通解为 p.d.TemplateBox[{p}, Inverse].{TemplateBox[{1}, CTraditional],TemplateBox[{2}, CTraditional],TemplateBox[{3}, CTraditional]}：

    使用 DSolveValue 验证解：

    假设一个粒子在平面力场中运动，其位置向量 满足 且 ，其中 和 为如下. 当 时求解初始问题：

    首先，计算 的特征值和对应的特征向量：

    方程组的通解为 . 使用 LinearSolve 确定系数：

    为特征向量构建线性组合：

    使用 DSolveValue 验证该解：

    当 是以下随机矩阵时，计算动力系统 的通解：

    求特征值和特征向量，使用 Chop 丢弃小数值误差：

    通解是形式为 的项的任意线性组合：

    验证 在数值舍入完成之前满足动力学方程：

    Lorenz 方程：

    求方程右边的雅可比行列式：

    求出平衡点：

    在第一个八分圆处求雅可比行列式的特征值和特征向量：

    沿 dir 方向上、 pt 中的向后小干扰积分函数：

    显示右侧平衡点的稳定曲线：

    求出左侧平衡点的稳定曲线：

    显示带有 Lorenz 方程解的稳定曲线：

    物理  (4)

    在量子力学中，状态由复单位向量表示，物理量由厄米特线性算子表示. 特征值表示可能的观测值，关于特征向量的分量的模的平方表示这些观测值的概率. 对于给定的自旋算子 和状态 ，找出可能的观测值及其概率：

    计算特征值，可能的观测值为 :

    找到特征向量并正规化以计算正确投影：

    的相对概率为 ， 的为 ：

    在量子力学中，能量算子称为哈密顿量 ，根据薛定谔方程 具有能量 的状态. 给定 方向上恒定磁场中自旋 1 粒子的哈密顿量，求处于初始状态 表示表示 的粒子在时间 的状态：

    计算特征值，能级为 和 ：

    求得并正规化特征向量：

    时间 的状态是根据薛定谔方程演化的每个特征态的总和：

    惯性矩是一个实对称矩阵，描述了刚体对不同方向旋转的阻力. 该矩阵的特征值称为主惯性矩，相应的特征向量（必须正交）称为主轴. 求下列四面体的主惯性矩和主轴：

    首先计算惯性矩：

    主矩是 的特征值：

    主轴为 的特征向量：

    验证轴为正交：

    四面体的质心在原点：

    可视化四面体及其主轴：

    广义特征系统可用于找到解耦项的耦合振荡的正规模. 思考图中所示的系统：

    根据胡克定律，该系统服从 , . 代入通解 得到矩阵方程 ，其中刚度矩阵 和质量矩阵 为如下：

    如果 , , 且 ，求特征频率和正规模：

    计算关于 的广义特征值 ：

    特征频率 是特征值的平方根：

    可从广义特征向量推导出模的形状：

    将正规模解构造为广义特征向量乘以相应指数：

    验证两者是否满足系统的微分方程：

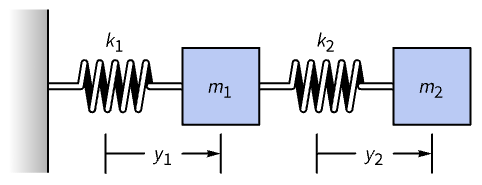
    属性和关系  (15)

    Eigenvalues[m] 实际上是 Eigensystem 返回配对的第一个元素：

    如果同时需要特征向量和特征值，仅调用 Eigensystem 通常会更有效：

    特征值是特征多项式的根：

    使用 CharacteristicPolynomial 计算多项式：

    验证是否相等：

    广义特征多项式由 TemplateBox[{{a, -, {b, , lambda}}}, Det] 给出:

    广义特征多项式只定义了有限特征值：

    无限广义特征值对应于 的特征向量 ，其中 ：

    m 的特征值的乘积等于 Det[m]：

    m 的特征值之和等于 Tr[m]：

    如果 所有特征值不同，则 DiagonalizableMatrixQ[m] 给出 True：

    反之为假：

    对于可逆矩阵 ，TemplateBox[{m}, Inverse] 的特征值是 的特征值的倒数：

    因为 Eigenvalues 按绝对值排序，所以会给出相同的值但相反的顺序：

    对于解析函数 ，将 应用于 的特征值 即会得到 的特征值：

    例如， 的特征值为 ：

    同样， 的特征值为 ：

    实对称矩阵的特征值是实数：

    任何埃尔米特矩阵的特征值也是如此：

    实反对称矩阵的特征值是虚数：

    任何反埃尔米特矩阵的特征值也是如此：

    正交矩阵的特征值位于单位圆上：

    任何酉矩阵的特征值也是如此：

    SingularValueList[m] 等于非零特征值 TemplateBox[{m}, ConjugateTranspose].m 的平方根：

    思考一个具有一组完整特征向量的矩阵 m：

    JordanDecomposition[m] 返回由特征值和特征向量构建的矩阵 {s,j}：

    j 矩阵是具有特征值项的对角矩阵，但可能与 Eigensystem 的顺序不同：

    对于数值正规矩阵 n，SchurDecomposition[n,RealBlockDiagonalFormFalse]：

    t 矩阵是有特征值项的对角矩阵，可能与 Eigensystem 的顺序不同：

    如果矩阵共用维度为 的零空间，则其广义特征值的 为 Indeterminate：

    关于自身的两个广义特征值为 Indeterminate：

    矩阵 有一维零空间：

    其位于 的零空间中：

    因此， 关于 的广义特征值为 Indeterminate：

    可能存在的问题  (5)

    Eigenvalues 和 Eigenvectors 不能保证绝对按相应顺序给出结果：

    第六个和第七个特征值基本上相等但正负相反：

    在此特定情况下，第七个特征向量不对应于第七个特征值：

    它对应的是第六个特征值：

    用 Eigensystem[mat] 确保相应的结果始终匹配：

    符号的例子，迅速得到很复杂的解：

    表达式个数呈指数级增长：

    20×20 的 Hilbert 矩阵：

    计算最小特征值的数值解：

    以机器精度计算最小特征值：

    最小和最大特征值间无关联：

    足够的数值计算精度：

    当特征值紧密分组时，稀疏矩阵的迭代方法不收敛：

    迭代在1000次后没有收敛：

    您可以对算法平移到期望值，以加速收敛：

    不包括为 FEAST 方法指定的区间的端点. 设置一个特征值为 3 和 9 的矩阵：

    在区间 内求特征值不能返回端点处的值：

    将区间扩大至 ，FEAST 即可找到特征值 3 和 9：

    Wolfram Research (1988)，Eigenvalues，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Eigenvalues.html （更新于 2024 年）.

    文本

    Wolfram Research (1988)，Eigenvalues，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Eigenvalues.html （更新于 2024 年）.

    CMS

    Wolfram 语言. 1988. "Eigenvalues." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Eigenvalues.html.

    APA

    Wolfram 语言. (1988). Eigenvalues. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Eigenvalues.html 年

    BibTeX

    @misc{reference.wolfram_2024_eigenvalues, author="Wolfram Research", title="{Eigenvalues}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Eigenvalues.html}", note=[Accessed: 10-October-2024 ]}

    BibLaTeX

    @online{reference.wolfram_2024_eigenvalues, organization={Wolfram Research}, title={Eigenvalues}, year={2024}, url={https://reference.wolfram.com/language/ref/Eigenvalues.html}, note=[Accessed: 10-October-2024 ]}