Jordan decomposition of a machine-precision matrix:

Format the results:

Jordan decomposition of a complex matrix:

Jordan decomposition of an exact matrix with a deficient eigenspace:

The one in the third column of indicates that the eigenspace corresponding to 48 is deficient:

The third column of is therefore a generalized eigenvector where gives rather than :

Jordan decomposition of an arbitrary-precision matrix:

Jordan decomposition of a symbolic matrix:

The Jordan decomposition of large numerical matrices is computed efficiently:

Jordan decomposition of sparse matrices:

Eigensystems of structured matrices:

IdentityMatrix is a Jordan canonical form:

The associated similarity matrix is a square root of the identity:

Jordan decomposition of a HilbertMatrix:

For the matrix , interpret the columns of the matrix of the Jordan decomposition in terms of true eigenvectors and generalized eigenvectors:

Compute the Jordan decomposition:

Columns of for which there is no above the diagonal in the corresponding of —columns 1, 3 and 4—are true eigenvectors for which :

The remaining column is a generalized eigenvector for which :

Show that the following matrix only has a single eigenvector, but it has a complete chain of generalized eigenvectors that form a basis for :

Eigensystem shows 84 is an eigenvalue of multiplicity 4 that has just one independent eigenvector:

The first column of the matrix of JordanDecomposition is the one eigenvector found:

The remaining columns are a chain for which :

Since has an empty NullSpace, its columns form a basis for :

A square matrix has a complete set of eigenvectors, and thus is diagonalizable, iff its matrix is diagonal:

Test if a particular matrix is diagonalizable:

Confirm using DiagonalizableMatrixQ:

Estimate the probability that a 4×4 matrix of ones and zeros will be diagonalizable:

An × matrix is nilpotent if for some :

Consider a non-diagonalizable matrix :

can be written as a sum of a diagonalizable matrix and a nilpotent matrix using JordanDecomposition:

Let be the matrix formed from and the diagonal part of :

Let be the matrix formed from and the superdiagonal part of :

Then is the sum of and :

The matrix is diagonalizable:

The matrix is nilpotent:

Moreover, the matrices and commute:

For a diagonalizable matrix, the Jordan decomposition directly gives a diagonalization as . Apply this to diagonalize the matrix :

Compute the Jordan decomposition:

Confirm the diagonalization:

Let be the linear transformation whose standard matrix is given by the matrix . Find a basis for with the property that the representation of in that basis is diagonal:

Find the Jordan decomposition of :

Let consist of the eigenvectors, i.e the columns of . As converts from -coordinates to standard coordinates, its inverse converts in the reverse direction:

Thus is given by , which is diagonal:

Note that this is simply the diagonal matrix whose entries are the eigenvalues:

A real-valued symmetric matrix is orthogonally diagonalizable as , with diagonal and real valued and orthogonal. Verify that the following matrix is symmetric and then diagonalize it:

Compute the Jordan decomposition:

Let equal :

Let equal after normalizing its columns:

Confirm that is indeed orthogonal:

Verify that :

A matrix is called normal if . Normal matrices are the most general kind of matrix that can be diagonalized by a unitary transformation. All real symmetric matrices are normal because both sides of the equality are simply :

Show that the following matrix is normal, then diagonalize it:

Confirm using NormalMatrixQ:

Compute the Jordan decomposition:

Unlike a real symmetric matrix, the diagonal matrix is complex valued:

Normalizing the columns of gives a unitary matrix:

Confirm the diagonalization :

Use the Jordan decomposition to compute and for the following matrix :

Compute the and matrices:

Confirm the identity :

Then . Since is upper triangular and nearly diagonal, the diagonal entries are raised to the power , and the entry becomes :

Thus, the expression for is:

Confirm with direct computation by MatrixPower:

Applying the power series for the exponential, the diagonal entries obviously become , and the off-diagonal term is merely a re-indexed exponential sum. Thus, it too becomes :

Thus, the expression for is:

Confirm using a direction computation by MatrixExp:

Confirm the formula 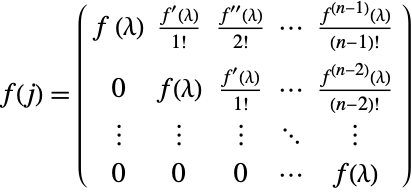for a Jordan matrix consisting of a single chain for the following matrix and the functions , and :

First compute the formula for :

Verify the computation using MatrixFunction:

The computation for is analogous:

MatrixFunction confirms the result:

As has a parameter, it is necessary to use D instead of Derivative and substitute in :

Again, MatrixFunction confirms the result when is entered using Function:

Solve the system of ODEs , , . First, construct the coefficient matrix for the right-hand side:

Compute the Jordan decomposition of :

Using the formula of the previous example, is given by:

The general solution is , for three arbitrary starting values:

Verify the solution using DSolveValue:

Produce the general solution of the dynamical system when is the following stochastic matrix:

Compute the Jordan decomposition of :

Since the is diagonal, consists of merely raising the diagonal entries to the power :

The general solution is :

Verify that satisfies the dynamical equation: