Minors

gives the minors of a matrix m.

gives the k minors.

Minors[m,k,f]

applies the function f rather than Det to each of the submatrices picked out.

Details

For an 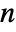× 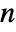matrix the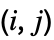 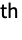element of Minors[m] gives the determinant of the matrix obtained by deleting the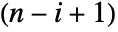 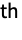row and the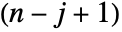 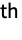column of m. »
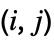
Reverse[Minors[m],{1,2}] makes the 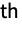element correspond to deleting the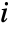 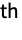row and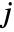 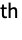column of m. »
Minors[m] is equivalent to Minors[m,Min[Dimensions[m]]-1]. »
Minors[m,k] gives the determinants of the k×k submatrices obtained by picking each possible set of k rows and k columns from m.
Each element in the result corresponds to taking rows and columns with particular lists of positions. The ordering of the elements is such that reading across or down the final matrix, the successive lists of positions appear in lexicographic order.
For an 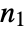× 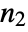matrix, Minors[m,k] gives an 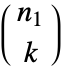× 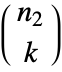matrix.

Examples

open allclose all

Basic Examples (2)

Minors of a 3×3 matrix:

2×2 minors of a 2×3 matrix:

Scope (14)

Basic Uses (6)

Find the minors of a machine-precision matrix:

Minors of a complex matrix:

Minors of an exact matrix:

Minors of an arbitrary-precision matrix:

Minors of a symbolic matrix:

Minors of a rectangular matrix:

Specifying the Minors Size (4)

Minors of a 4×4 matrix:

These are the 3rd minors:

The matrices used to compute the minors:

The dimensions of Minors[m,k] for the allowed values of k for a 4×4 matrix:

Though Minors[m,0] and Minors[m,4] have the same dimensions, they are different matrices:

Note that Minors[m,4] equals {{Det[m]}}:

Similarly, Minors[m,1] and Minors[m,3] are different matrices:

Note that Minors[m,3] equals Minors[m]:

Minors[m,2] has the largest dimensions:

2×2 minors of a 3×4 matrix:

The matrices used to compute the minors:

The dimensions of Minors[m,k] for the allowed values of k for a 3×4 matrix:

Display the various minors:

Special Matrices (4)

Minors of a sparse matrix:

Minors of structured matrices:

IdentityMatrix[n] is not changed by Minors:

For different values of k, it gives an identity matrix of the appropriate size:

Minors of HilbertMatrix:

Applications (5)

Visualize the determinants used to compute Minors[m] for a square matrix:

Reverse both levels of m to get the entry to come from deleting the row and column:

Compute the cofactor matrix:

The adjugate matrix is its transpose:

Compare with the result returned by Adjugate:

Compute the rank of a matrix:

The rank is the largest k for which Minors[mat,k] contains nonzero entries:

Use MatrixRank to check that the rank is indeed equal to two:

Test if a Hermitian matrix is positive definite using Sylvester's criterion:

Since all of the leading principle minors are positive, the matrix is positive definite:

Confirm the result using PositiveDefiniteMatrixQ:

Find the singularities of an algebraic space curve:

The curve is the intersection of two surfaces:

Generate an explicit parametrization of the curve:

Properties & Relations (11)

For an matrix, Minors[m] is the matrix of determinants found by deleting row and column :

Reverse[Minors[m],{1,2}] is the matrix of determinants found by deleting the row and column of m:

For an matrix and a fixed from 1 to , $TemplateBox[{m}, Det]=sum_(k=1)^n(-1)^(2 n-i-k) m_(n+1-i,n+1-k) Minors[m]_(i,k)$ :

With r=Reverse[Minors[m],{1,2}], this can be expressed as $TemplateBox[{m}, Det]=sum_(k=1)^n(-1)^(i+k) m_(i,k) r_(i,k)$ :

The transposed equality $TemplateBox[{m}, Det]=sum_(k=1)^n(-1)^(2 n-i-k) m_(n+1-k,n+1-i) Minors[m]_(k,i)$ also holds:

Minors[m] is equivalent to Minors[m]==Minors[m,Min[Dimensions[m]]-1]:

For a square matrix m, Minors[m,Length[m]] equals {{Det[m]}}:

By definition, Minors[m,0] is {{1}}:

Minors of dimension higher than the MatrixRank are zero:

The Dimensions of the minors of an × matrix are ×:

Minors of a square identity matrix is another identity matrix:

This is not true of rectangular identity matrices:

Minors of a square diagonal matrix is another diagonal matrix:

Minors is effectively equivalent to an outer product of row and column extractions:

Neat Examples (1)

Some minor variations:

Top

Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how