Adjugate[m]
gives the adjugate of a square matrix m.


Adjugate
Adjugate[m]
gives the adjugate of a square matrix m.
Details
- The adjugate is also known as the classical adjoint or the adjunct matrix.
- The adjugate of an invertible matrix m is given by Inverse[m]Det[m].
- The matrix product of a matrix m with its adjugate is equal to the determinant of m multiplied by an identity matrix of the same size as m.
- The matrix m can be numerical or symbolic, but must be square.
- Adjugate[m] formats as
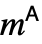 in StandardForm and TraditionalForm. »
in StandardForm and TraditionalForm. »
Examples
open all close allBasic Examples (3)
Scope (10)
Basic Uses (6)
Applications (4)
Compute a cofactor using Adjugate:
Compute the inverse of a matrix using Adjugate:
Compare with Inverse:
Use Adjugate to solve a linear equation:
Compare with LinearSolve:
Define a function for computing the Gaussian curvature of a surface represented as an implicit Cartesian equation:
The implicit Cartesian equation of a surface with icosahedral symmetry:
Compute its Gaussian curvature:
Visualize regions of positive (red) and negative (blue) Gaussian curvature on the surface:
Properties & Relations (5)
m.Adjugate[m] is equal to Det[m] times an identity matrix of the same size:
Inverse[m] is equal to the adjugate divided by the determinant:
For an n×n matrix m, Adjugate[m] equals LinearSolve[m,Det[m]IdentityMatrix[n]]:
Neat Examples (2)
Define a function for computing the adjugate polynomial of a square matrix:
Compute the adjugate polynomial of a matrix:
Evaluating the adjugate polynomial of a matrix at the matrix itself gives the adjugate:
Define a function for computing the iterated adjugate of a square matrix:
Tech Notes
Related Guides
History
Text
Wolfram Research (2021), Adjugate, Wolfram Language function, https://reference.wolfram.com/language/ref/Adjugate.html.
CMS
Wolfram Language. 2021. "Adjugate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Adjugate.html.
APA
Wolfram Language. (2021). Adjugate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Adjugate.html
BibTeX
@misc{reference.wolfram_2025_adjugate, author="Wolfram Research", title="{Adjugate}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Adjugate.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_adjugate, organization={Wolfram Research}, title={Adjugate}, year={2021}, url={https://reference.wolfram.com/language/ref/Adjugate.html}, note=[Accessed: 25-January-2026]}