JordanMatrix
JordanMatrix[λ,n]
returns a Jordan matrix with dimension n and diagonal elements λ.
JordanMatrix[λ,n,dir]
returns a Jordan matrix oriented by specification dir.
Details
- Jordan matrices provide the building blocks for the Jordan decomposition of a matrix.
- JordanMatrix by default returns an n×n matrix
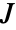with diagonal elements equal to λ and superdiagonal elements equal to 1. -
J=(
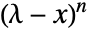
)λ 1 0 … 0 0 λ 1 ⋱ 0 0 0 λ ⋱ ⋮ ⋮ ⋮ ⋱ ⋱ 1 0 0 … 0 λ - CharacteristicPolynomial[J,x] is
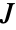. Up to sign, so is MatrixMinimalPolynomial[J,x]. » - The Jordan matrix
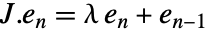occurs naturally for cyclic subspaces: » 
, …, 
, 
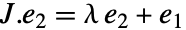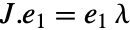- where
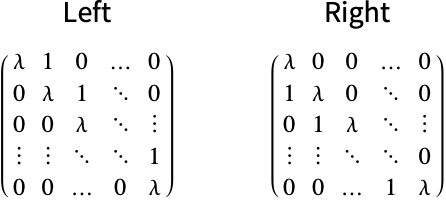
is UnitVector[n,i]. JordanDecomposition returns a block Jordan matrix of this form. » - JordanMatrix[λ,n,dir] uses dir to determine the resulting matrix layout. It must be one of Left (the default) or Right. This directive determines whether the diagonal elements are to the left or right respective to the 1s. »
- The following options can be given:
-
TargetStructure Automatic the structure of the returned matrix - Possible settings for TargetStructure include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Sparse" represent the matrix as a sparse array "Structured" represent the matrix as a structured array
Examples
open all close all
Scope (4)
The first argument can be any numeric expression:
The first argument can be any purely symbolic expression:
The first argument must be a scalar:
JordanMatrix defaults to the orientation specification Left:
Options (2)
TargetStructure (2)
By default, JordanMatrix returns a dense matrix:
Instead return a SparseArray:
Check that it corresponds to the dense result:
Return an array structured as an upper triangular matrix:
Check that it corresponds to the dense result:
For TargetStructure"Structured", the type of structure depends on the direction argument:
Using Right changes the type from UpperTriangularMatrix to LowerTriangularMatrix:
Applications (1)
Construct a matrix m of nonzero entries with a double deficient eigenspace, a singly deficient eigenspace, and a non-deficient rank-two eigenspace. Compare the Jordan decomposition of m with the matrices used to build m. First, define a 
Jordan matrix to represent the doubly deficient eigenspace:
Next, create a 
Jordan matrix for the singly deficient space:
Finally, create a 
diagonal matrix for the full-rank space:
Combine these blocks into a single matrix using BlockDiagonalMatrix:
Using a similarity matrix with positive entries is likely to give nonzero entries; the following s in fact does:
The eigenvalues match the diagonal entries and dimensions of the three Jordan matrices used to build m:
The zero rows 2 and 3 of vecs show that 5 is doubly deficient, and row 5 shows that 4 is singly deficient:
Now compute JordanDecomposition[m]:
The similarity matrix computed is quite different from s—similarity matrices are not unique:
The computed Jordan matrix also differs from j:
But closer inspection shows that the blocks simply appear in different orders:
If the blocks are ordered by absolute value of the eigenvalue, the matrices are the same:
Properties & Relations (7)
CharacteristicPolynomial[JordanMatrix[λ,n],x] is 
:
MatrixMinimalPolynomial[JordanMatrix[λ,n],x] is 
:
A Jordan matrix is defined by 
for 
and 
:
With the orientation Right, the relations are 
for 
and 
:
The vectors 
, 
, 
, 
, 
are linearly independent:
With the orientation Right, the chain begins at 
rather than 
:
In more than one dimension, a Jordan matrix is non-diagonalizable:
The one dimensional case is an exception as all 1×1 matrices are diagonal:
In more than one dimension, a Jordan matrix is not normal:
The determinant of JordanMatrix[λ,n] is 
:
Thus, the Jordan matrix is invertible if 
:
The Jordan matrix returned by JordanDecomposition is block diagonal:
Each block is of the form JordanMatrix[λ,k] for some k:
Show that the diagonal entries of j are the eigenvalues of m, possibly in a different order:
Text
Wolfram Research (2025), JordanMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanMatrix.html.
CMS
Wolfram Language. 2025. "JordanMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JordanMatrix.html.
APA
Wolfram Language. (2025). JordanMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanMatrix.html