gives the minimal polynomial for the square matrix m in the variable x.


MatrixMinimalPolynomial
gives the minimal polynomial for the square matrix m in the variable x.
Details and Options
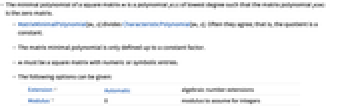
- The minimal polynomial of a square matrix m is a polynomial
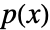 of lowest degree such that the matrix polynomial
of lowest degree such that the matrix polynomial 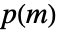 is the zero matrix. »
is the zero matrix. » - MatrixMinimalPolynomial[m,x] divides CharacteristicPolynomial[m,x]. Often they agree; that is, the quotient is a constant. »
- The matrix minimal polynomial is only defined up to a constant factor. »
- m must be a square matrix with numeric or symbolic entries.
- The following options can be given:
-
Extension Automatic algebraic number extensions Modulus 0 prime modulus to use - MatrixMinimalPolynomial[m,Modulusp] computes the polynomial modulo the prime p. If p is zero, ordinary arithmetic is used. »
Examples
open all close allBasic Examples (2)
Scope (10)
Basic Uses (5)
Special Matrices (5)
Minimal polynomials of sparse matrices:
Minimal polynomials of structured matrices:
The minimal polynomial of a diagonal matrix has linear terms in the distinct diagonal entries:
For multiples of the identity matrix, this becomes a single linear factor:
The minimal polynomial of JordanMatrix[λ,n]:
The polynomial is proportional to ![]() :
:
The minimal polynomial of CompanionMatrix[{c0,c1,…,cn}}]:
Options (3)
Modulus (1)
Extension (2)
Compute a minimal polynomial where some matrix elements depend on algebraic numbers:
The algebraic relations can be interpreted as replacing t1 with and t2 with ![]() :
:
Compare this to a direct computation using these algebraic numbers explicitly:
Find the minimal polynomial of a matrix that has a parameter as well as an algebraic extension:
Applications (2)
The factored form of the matrix minimal polynomial gives important information about the eigenspaces of the matrix. Namely, it indicates how much larger the generalized eigenspace for ![]() is than its ordinary eigenspace. Consider the follow matrix
is than its ordinary eigenspace. Consider the follow matrix ![]() :
:
Compute its minimal polynomial ![]() :
:
And its characteristic polynomial ![]() :
:
Because ![]() has a linear term in
has a linear term in ![]() , its generalized and ordinary eigenspaces are equal. The eigenspace is:
, its generalized and ordinary eigenspaces are equal. The eigenspace is:
The geometric multiplicity of ![]() ,
, ![]() , matches its algebraic multiplicity, the power of
, matches its algebraic multiplicity, the power of ![]() in
in ![]() :
:
Confirm the generalized eigenspace is the ordinary eigenspace by showing ![]() and
and ![]() have the same null spaces:
have the same null spaces:
The presence of ![]() in
in ![]() means
means ![]() has a larger null space than
has a larger null space than ![]() :
:
The generalized eigenspace is now larger than the ordinary eigenspace:
Since the algebraic multiplicity of ![]() is
is ![]() , higher powers of
, higher powers of ![]() have the same null space:
have the same null space:
Finally, the presence of ![]() in
in ![]() means that
means that ![]() has larger null spaces for
has larger null spaces for ![]() and
and ![]() but not
but not ![]() :
:
Use the minimal polynomial to compute the DrazinInverse:
The coefficients can be used to compute the Drazin inverse:
Verify some properties of the Drazin inverse:
Compare with the result of DrazinInverse:
Properties & Relations (6)
The minimal polynomial of ![]() is the lowest-order polynomial
is the lowest-order polynomial ![]() for which
for which ![]() yields a zero matrix:
yields a zero matrix:
Confirm that ![]() is an
is an ![]() zero matrix:
zero matrix:
Since ![]() is quintic, no quadric (or lower-order) polynomial can give zero when evaluated at
is quintic, no quadric (or lower-order) polynomial can give zero when evaluated at ![]() :
:
The degree of a matrix minimal polynomial can be anywhere from 1 to the matrix dimension n:
This is different from the characteristic polynomial, which always has degree n:
The minimal polynomial divides the characteristic polynomial with a (possibly constant) polynomial quotient:
The minimal polynomial and the characteristic polynomial have the same distinct roots:
In particular, this means ![]() divides
divides ![]() raised to the
raised to the ![]() power:
power:
A matrix minimal polynomial is often the same as the characteristic polynomial up to a constant factor:
Estimate the fraction of zero–one ![]() matrices for which this is true:
matrices for which this is true:
The last element in the diagonal of the Smith normal form of a characteristic matrix gives the minimal polynomial:
Find the last block in the Frobenius normal form:
This gives the negatives of the minimal polynomial coefficients with lead coefficient implicitly set to 1:
Possible Issues (1)
The polynomial returned by MatrixMinimalPolynomial is generally monic for exact input:
Related Guides
History
Text
Wolfram Research (2025), MatrixMinimalPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/MatrixMinimalPolynomial.html.
CMS
Wolfram Language. 2025. "MatrixMinimalPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixMinimalPolynomial.html.
APA
Wolfram Language. (2025). MatrixMinimalPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixMinimalPolynomial.html
BibTeX
@misc{reference.wolfram_2025_matrixminimalpolynomial, author="Wolfram Research", title="{MatrixMinimalPolynomial}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixMinimalPolynomial.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_matrixminimalpolynomial, organization={Wolfram Research}, title={MatrixMinimalPolynomial}, year={2025}, url={https://reference.wolfram.com/language/ref/MatrixMinimalPolynomial.html}, note=[Accessed: 16-January-2026]}