WOLFRAM

Wolfram Language & System Documentation Center

Extension

is an option for various polynomial and algebraic functions that specifies generators for the algebraic number field to be used.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Properties & Relations  
See Also
Tech Notes
Related Guides
History
Cite this Page

Extension

Extension

is an option for various polynomial and algebraic functions that specifies generators for the algebraic number field to be used.

Details

  • For polynomial functions, Extension determines the algebraic number field in which the coefficients are assumed to lie.
  • The setting Extension->a specifies the field 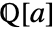consisting of the rationals extended by the algebraic number a.
  • Extension->{a1,a2,…} specifies the field .
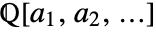  • The ai must be exact numbers, and can involve radicals as well as Root and AlgebraicNumber objects.
  • Extension->Automatic specifies that any algebraic numbers that appear in the input should be included in the extension field.
  • For polynomial functions, the default setting Extension->None specifies that all coefficients are required to be rational. Any algebraic numbers appearing in input are treated like independent variables.
  • Extension->{a1,a2,…} includes both the ai and any algebraic numbers in the input.
  • GaussianIntegers->True is equivalent to Extension->I.

Examples

open all close all

Basic Examples  (2)

Factor a polynomial over :

PolynomialGCD over the field generated by the algebraic numbers present in the coefficients:

Scope  (8)

By default, factorization is performed over the rationals:

This specifies the factorization should be done over the rationals extended by :

Here the factorization is done over the rationals extended by and I:

By default, PolynomialGCD treats algebraic numbers as independent variables:

This computes the GCD over the algebraic number field generated by the coefficients:

By default, Together treats algebraic numbers as independent variables:

With Extension->Automatic, Together recognizes algebraically dependent coefficients:

By default, the norm is computed in the field generated by the AlgebraicNumber object:

This computes the norm in the field in which the AlgebraicNumber object is represented:

This computes the norm in the field generated by :

Properties & Relations  (1)

For Factor, Extension->I is equivalent to GaussianIntegers->True:

Wolfram Research (1996), Extension, Wolfram Language function, https://reference.wolfram.com/language/ref/Extension.html (updated 2007).

Text

Wolfram Research (1996), Extension, Wolfram Language function, https://reference.wolfram.com/language/ref/Extension.html (updated 2007).

CMS

Wolfram Language. 1996. "Extension." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Extension.html.

APA

Wolfram Language. (1996). Extension. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Extension.html

BibTeX

@misc{reference.wolfram_2025_extension, author="Wolfram Research", title="{Extension}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Extension.html}", note=[Accessed: 14-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_extension, organization={Wolfram Research}, title={Extension}, year={2007}, url={https://reference.wolfram.com/language/ref/Extension.html}, note=[Accessed: 14-August-2025]}