is an option for FactorInteger, PrimeQ, Factor, and related functions that specifies whether factorization should be done over Gaussian integers.


GaussianIntegers
is an option for FactorInteger, PrimeQ, Factor, and related functions that specifies whether factorization should be done over Gaussian integers.
Details
- With GaussianIntegers->False, factorization is done over the ordinary ring of integers
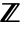 .
. - With GaussianIntegers->True, factorization is done over the ring of integers with i adjoined
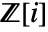 .
. - The Gaussian primes used when GaussianIntegers->True are chosen to have both real and imaginary parts positive.
- The first entry in the list given by FactorInteger with GaussianIntegers->True may be -1 or -I.
Examples
open all close allScope (3)
By default polynomial factorization is performed over the rationals:
This specifies that the factorization should be done over ![]() :
:
By default integer factorization is performed over the integers:
This specifies that the factorization should be done over the Gaussian integers:
A number prime over the integers may not be prime over the Gaussian integers:
Properties & Relations (1)
For Factor, GaussianIntegers->True is equivalent to Extension->I:
Related Guides
History
Introduced in 1991 (2.0)
Text
Wolfram Research (1991), GaussianIntegers, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianIntegers.html.
CMS
Wolfram Language. 1991. "GaussianIntegers." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GaussianIntegers.html.
APA
Wolfram Language. (1991). GaussianIntegers. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianIntegers.html
BibTeX
@misc{reference.wolfram_2025_gaussianintegers, author="Wolfram Research", title="{GaussianIntegers}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianIntegers.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_gaussianintegers, organization={Wolfram Research}, title={GaussianIntegers}, year={1991}, url={https://reference.wolfram.com/language/ref/GaussianIntegers.html}, note=[Accessed: 17-January-2026]}